dorogovtsev_goltsev_mendes_graph

dorogovtsev_goltsev_mendes_graph(n, create_using=None)

Returns the hierarchically constructed Dorogovtsev–Goltsev–Mendes graph.

The Dorogovtsev–Goltsev–Mendes [1] procedure deterministically produces a scale-free graph with 3/2 * (3**(n-1) + 1) nodes and 3**n edges for a given n.

Note that n denotes the number of times the state transition is applied, starting from the base graph with n = 0 (no transitions), as in [2]. This is different from the parameter t = n - 1 in [1].

(Source code, png)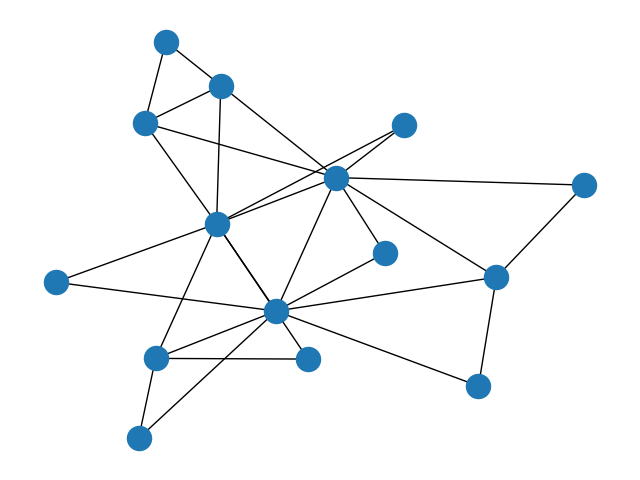

Parameters:

ninteger

The generation number.

create_usingNetworkX graph constructor, optional (default=nx.Graph)

Graph type to create. Directed graphs and multigraphs are not supported.

Returns:

GNetworkX Graph

Raises:

NetworkXError

If n is less than zero.

If create_using is a directed graph or multigraph.

References

[1] (1,2)

S. N. Dorogovtsev, A. V. Goltsev and J. F. F. Mendes, “Pseudofractal scale-free web”, Physical Review E 65, 066122, 2002. https://arxiv.org/pdf/cond-mat/0112143.pdf

[2]

Weisstein, Eric W. “Dorogovtsev–Goltsev–Mendes Graph”. From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/Dorogovtsev-Goltsev-MendesGraph.html

Examples

>>> G = nx.dorogovtsev_goltsev_mendes_graph(3)
>>> G.number_of_nodes()
15
>>> G.number_of_edges()
27
>>> nx.is_planar(G)
True