dorogovtsev_goltsev_mendes_graph#
- dorogovtsev_goltsev_mendes_graph(n, create_using=None)[source]#
Returns the hierarchically constructed Dorogovtsev–Goltsev–Mendes graph.
The Dorogovtsev–Goltsev–Mendes [1] procedure deterministically produces a scale-free graph with
3/2 * (3**(n-1) + 1)nodes and3**nedges for a givenn.Note that
ndenotes the number of times the state transition is applied, starting from the base graph withn = 0(no transitions), as in [2]. This is different from the parametert = n - 1in [1].(
Source code,png)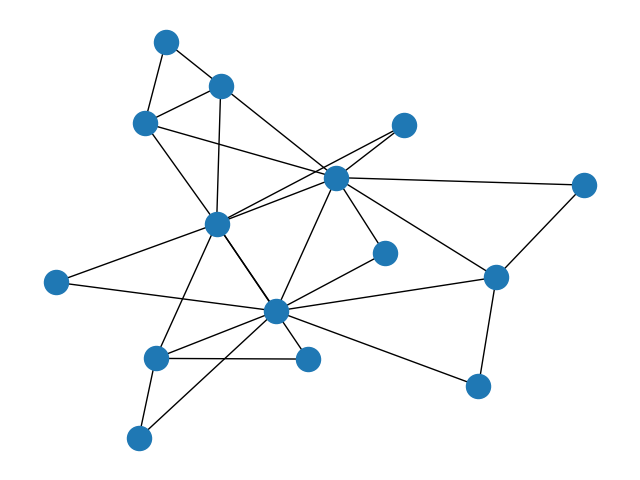
- Parameters:
- ninteger
The generation number.
- create_usingNetworkX graph constructor, optional (default=nx.Graph)
Graph type to create. Directed graphs and multigraphs are not supported.
- Returns:
- GNetworkX
Graph
- GNetworkX
- Raises:
- NetworkXError
If
nis less than zero.If
create_usingis a directed graph or multigraph.
References
[1] (1,2)S. N. Dorogovtsev, A. V. Goltsev and J. F. F. Mendes, “Pseudofractal scale-free web”, Physical Review E 65, 066122, 2002. https://arxiv.org/pdf/cond-mat/0112143.pdf
[2]Weisstein, Eric W. “Dorogovtsev–Goltsev–Mendes Graph”. From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/Dorogovtsev-Goltsev-MendesGraph.html
Examples
>>> G = nx.dorogovtsev_goltsev_mendes_graph(3) >>> G.number_of_nodes() 15 >>> G.number_of_edges() 27 >>> nx.is_planar(G) True