Note
Go to the end to download the full example code.
Maximum Independent Set#
An independent set is a set of vertices in a graph where no two vertices in the set are adjacent. The maximum independent set is the independent set of largest possible size for a given graph.
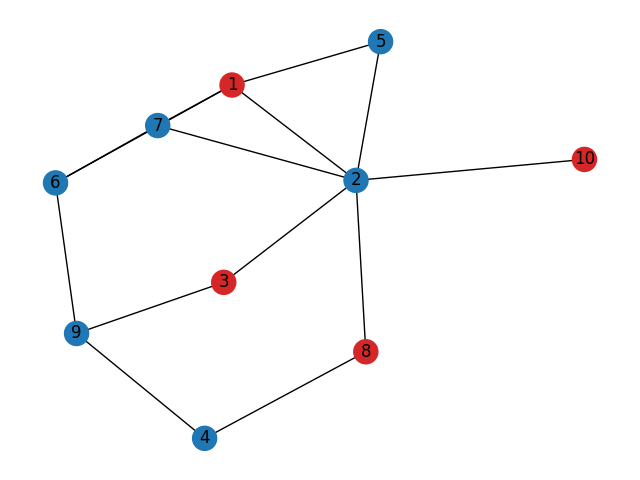
Maximum independent set of G: {8, 1, 10, 3}
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
from networkx.algorithms import approximation as approx
G = nx.Graph(
[
(1, 2),
(7, 2),
(3, 9),
(3, 2),
(7, 6),
(5, 2),
(1, 5),
(2, 8),
(10, 2),
(1, 7),
(6, 1),
(6, 9),
(8, 4),
(9, 4),
]
)
I = approx.maximum_independent_set(G)
print(f"Maximum independent set of G: {I}")
pos = nx.spring_layout(G, iterations=100, seed=42)
nx.draw(
G,
pos=pos,
with_labels=True,
node_color=["tab:red" if n in I else "tab:blue" for n in G],
)
Total running time of the script: (0 minutes 0.036 seconds)