Bipartite Motifs: α/β-core

The alpha-beta core of a bipartite graph is a maximal subgraph where each node in the top set has at least alpha neighbors and each node in bottom set has at least beta neightbors.

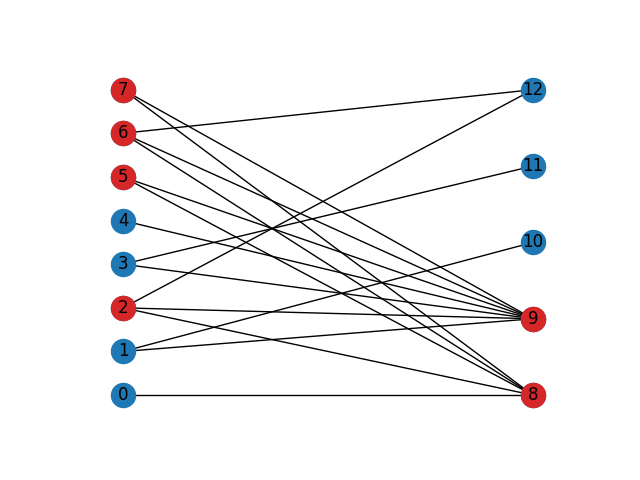
Nodes comprising the α(2)/β(3)-core of G: {2, 5, 6, 7, 8, 9}

import networkx as nx
import matplotlib.pyplot as plt

# A connected bipartite graph
G = nx.bipartite.havel_hakimi_graph(
    [1, 2, 3, 2, 1, 2, 3, 2], [5, 7, 1, 1, 2], create_using=nx.Graph
)
U, V = nx.bipartite.sets(G)


# Compute the alpha/beta-core of G
alpha, beta = 2, 3
G_core = G.copy()
while remove_nodes := [
    n for n, d in G_core.degree() if ((n in U and d < alpha) or (n in V and d < beta))
]:
    G_core.remove_nodes_from(remove_nodes)
print(f"Nodes comprising the α({alpha})/β({beta})-core of G: {set(G_core.nodes)}")

# Visualize the graph
fig, ax = plt.subplots()
pos = nx.bipartite_layout(G, nodes=U)
nx.draw(G, pos=pos, ax=ax, with_labels=True)
# Highlight the nodes of the a/b core in red
nx.draw_networkx_nodes(G, pos=pos, nodelist=list(G_core), node_color="tab:red")
plt.show()