Note
Go to the end to download the full example code.
Minimum Spanning Tree#
A minimum spanning tree (MST) is a subset of edges in a weighted,
connected graph that connects all vertices together with the
minimum possible total edge weight. The minimum_spanning_tree
function is used to compare the original graph with its MST.
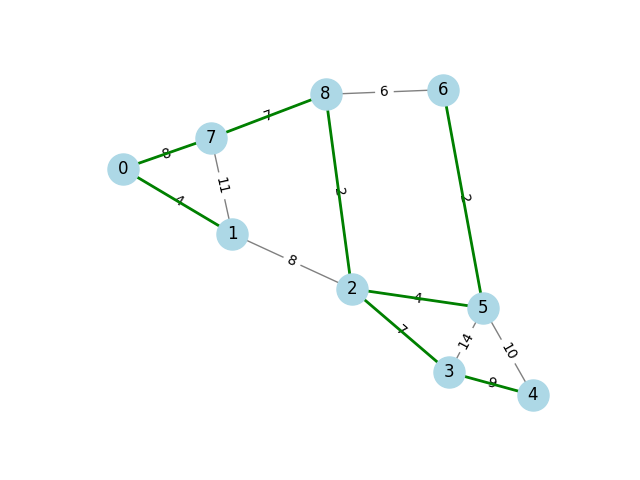
import networkx as nx
import matplotlib.pyplot as plt
# Create a graph
G = nx.Graph()
G.add_edges_from(
[
(0, 1, {"weight": 4}),
(0, 7, {"weight": 8}),
(1, 7, {"weight": 11}),
(1, 2, {"weight": 8}),
(2, 8, {"weight": 2}),
(2, 5, {"weight": 4}),
(2, 3, {"weight": 7}),
(3, 4, {"weight": 9}),
(3, 5, {"weight": 14}),
(4, 5, {"weight": 10}),
(5, 6, {"weight": 2}),
(6, 8, {"weight": 6}),
(7, 8, {"weight": 7}),
]
)
# Find the minimum spanning tree
T = nx.minimum_spanning_tree(G)
# Visualize the graph and the minimum spanning tree
pos = nx.spring_layout(G)
nx.draw_networkx_nodes(G, pos, node_color="lightblue", node_size=500)
nx.draw_networkx_edges(G, pos, edge_color="grey")
nx.draw_networkx_labels(G, pos, font_size=12, font_family="sans-serif")
nx.draw_networkx_edge_labels(
G, pos, edge_labels={(u, v): d["weight"] for u, v, d in G.edges(data=True)}
)
nx.draw_networkx_edges(T, pos, edge_color="green", width=2)
plt.axis("off")
plt.show()
Total running time of the script: (0 minutes 0.079 seconds)