node_redundancy¶

node_redundancy(G, nodes=None)[source]¶

Computes the node redundancy coefficients for the nodes in the bipartite graph G.

The redundancy coefficient of a node $v$ is the fraction of pairs of neighbors of $v$ that are both linked to other nodes. In a one-mode projection these nodes would be linked together even if $v$ were not there.

More formally, for any vertex $v$ , the redundancy coefficient of `v` is defined by

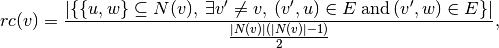
$rc(v) = \frac{|\{\{u, w\} \subseteq N(v), \: \exists v' \neq v,\: (v',u) \in E\: \mathrm{and}\: (v',w) \in E\}|}{ \frac{|N(v)|(|N(v)|-1)}{2}},$

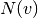where $N(v)$ is the set of neighbors of $v$ in G.

Parameters:	G (graph) – A bipartite graph nodes (list or iterable (optional)) – Compute redundancy for these nodes. The default is all nodes in G.
Returns:	redundancy – A dictionary keyed by node with the node redundancy value.
Return type:	dictionary

Examples

Compute the redundancy coefficient of each node in a graph:

>>> import networkx as nx
>>> from networkx.algorithms import bipartite
>>> G = nx.cycle_graph(4)
>>> rc = bipartite.node_redundancy(G)
>>> rc[0]
1.0

Compute the average redundancy for the graph:

>>> import networkx as nx
>>> from networkx.algorithms import bipartite
>>> G = nx.cycle_graph(4)
>>> rc = bipartite.node_redundancy(G)
>>> sum(rc.values()) / len(G)
1.0

Compute the average redundancy for a set of nodes:

>>> import networkx as nx
>>> from networkx.algorithms import bipartite
>>> G = nx.cycle_graph(4)
>>> rc = bipartite.node_redundancy(G)
>>> nodes = [0, 2]
>>> sum(rc[n] for n in nodes) / len(nodes)
1.0

Raises:	`NetworkXError` – If any of the nodes in the graph (or in `nodes`, if specified) has (out-)degree less than two (which would result in division by zero, according to the definition of the redundancy coefficient).

References

[1]	Latapy, Matthieu, Clémence Magnien, and Nathalie Del Vecchio (2008). Basic notions for the analysis of large two-mode networks. Social Networks 30(1), 31–48.