Warning
This documents an unmaintained version of NetworkX. Please upgrade to a maintained version and see the current NetworkX documentation.
robins_alexander_clustering¶
-
robins_alexander_clustering(G)[source]¶ Compute the bipartite clustering of G.
Robins and Alexander [1] defined bipartite clustering coefficient as four times the number of four cycles
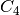 divided by the number of
three paths
divided by the number of
three paths 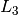 in a bipartite graph:
in a bipartite graph: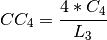
Parameters: G (graph) – a bipartite graph Returns: clustering – The Robins and Alexander bipartite clustering for the input graph. Return type: float Examples
>>> from networkx.algorithms import bipartite >>> G = nx.davis_southern_women_graph() >>> print(round(bipartite.robins_alexander_clustering(G), 3)) 0.468
See also
latapy_clustering(),square_clustering()References
[1] Robins, G. and M. Alexander (2004). Small worlds among interlocking directors: Network structure and distance in bipartite graphs. Computational & Mathematical Organization Theory 10(1), 69–94.