Warning
This documents an unmaintained version of NetworkX. Please upgrade to a maintained version and see the current NetworkX documentation.
Approximation¶
Connectivity¶
Fast approximation for node connectivity
all_pairs_node_connectivity(G[, nbunch, cutoff]) |
Compute node connectivity between all pairs of nodes. |
local_node_connectivity(G, source, target[, ...]) |
Compute node connectivity between source and target. |
node_connectivity(G[, s, t]) |
Returns an approximation for node connectivity for a graph or digraph G. |
K-components¶
Fast approximation for k-component structure
k_components(G[, min_density]) |
Returns the approximate k-component structure of a graph G. |
Clique¶
Cliques.
max_clique(G) |
Find the Maximum Clique |
clique_removal(G) |
Repeatedly remove cliques from the graph. |
Clustering¶
average_clustering(G[, trials]) |
Estimates the average clustering coefficient of G. |
Dominating Set¶
Functions for finding node and edge dominating sets.
A `dominating set`_[1] for an undirected graph *G with vertex set V and edge set E is a subset D of V such that every vertex not in D is adjacent to at least one member of D. An `edge dominating set`_[2] is a subset *F of E such that every edge not in F is incident to an endpoint of at least one edge in F.
| [1] | dominating set: https://en.wikipedia.org/wiki/Dominating_set |
| [2] | edge dominating set: https://en.wikipedia.org/wiki/Edge_dominating_set |
min_weighted_dominating_set(G[, weight]) |
Returns a dominating set that approximates the minimum weight node dominating set. |
min_edge_dominating_set(G) |
Return minimum cardinality edge dominating set. |
Independent Set¶
Independent Set
Independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I. The size of an independent set is the number of vertices it contains.
A maximum independent set is a largest independent set for a given graph G and its size is denoted α(G). The problem of finding such a set is called the maximum independent set problem and is an NP-hard optimization problem. As such, it is unlikely that there exists an efficient algorithm for finding a maximum independent set of a graph.
http://en.wikipedia.org/wiki/Independent_set_(graph_theory)
Independent set algorithm is based on the following paper:
 apx of maximum clique/independent set.
apx of maximum clique/independent set.
Boppana, R., & Halldórsson, M. M. (1992). Approximating maximum independent sets by excluding subgraphs. BIT Numerical Mathematics, 32(2), 180–196. Springer. doi:10.1007/BF01994876
maximum_independent_set(G) |
Return an approximate maximum independent set. |
Matching¶
Graph Matching¶
Given a graph G = (V,E), a matching M in G is a set of pairwise non-adjacent edges; that is, no two edges share a common vertex.
min_maximal_matching(G) |
Returns the minimum maximal matching of G. |
Vertex Cover¶
Vertex Cover¶
Given an undirected graph 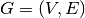 and a function w assigning nonnegative
weights to its vertices, find a minimum weight subset of V such that each edge
in E is incident to at least one vertex in the subset.
and a function w assigning nonnegative
weights to its vertices, find a minimum weight subset of V such that each edge
in E is incident to at least one vertex in the subset.
min_weighted_vertex_cover(G[, weight]) |
2-OPT Local Ratio for Minimum Weighted Vertex Cover |
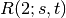 for graph.
for graph.