min_weighted_dominating_set¶

min_weighted_dominating_set(G, weight=None)[source]¶

Returns a dominating set that approximates the minimum weight node dominating set.

Parameters:	G (NetworkX graph) – Undirected graph. weight (string) – The node attribute storing the weight of an edge. If provided, the node attribute with this key must be a number for each node. If not provided, each node is assumed to have weight one.
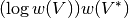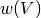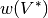Returns:	min_weight_dominating_set – A set of nodes, the sum of whose weights is no more than $(\log w(V)) w(V^)$ , where $w(V)$ denotes the sum of the weights of each node in the graph and $w(V^)$ denotes the sum of the weights of each node in the minimum weight dominating set.
Return type:	set

Notes

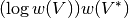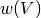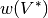This algorithm computes an approximate minimum weighted dominating set for the graph G. The returned solution has weight $(\log w(V)) w(V^*)$ , where $w(V)$ denotes the sum of the weights of each node in the graph and $w(V^*)$ denotes the sum of the weights of each node in the minimum weight dominating set for the graph.

This implementation of the algorithm runs in 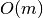$O(m)$ time, where 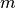$m$ is the number of edges in the graph.

References

[1]	Vazirani, Vijay V. Approximation Algorithms. Springer Science & Business Media, 2001.