Warning
This documents an unmaintained version of NetworkX. Please upgrade to a maintained version and see the current NetworkX documentation.
max_clique¶
-
max_clique(G)[source]¶ Find the Maximum Clique
Finds the
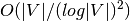 apx of maximum clique/independent set
in the worst case.
apx of maximum clique/independent set
in the worst case.Parameters: G (NetworkX graph) – Undirected graph Returns: - clique (set) – The apx-maximum clique of the graph
- Notes
- ——
- A clique in an undirected graph G = (V, E) is a subset of the vertex set
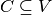 , such that for every two vertices in C, there exists an edge
, such that for every two vertices in C, there exists an edge- connecting the two. This is equivalent to saying that the subgraph
- induced by C is complete (in some cases, the term clique may also refer
- to the subgraph).
- A maximum clique is a clique of the largest possible size in a given graph.
- The clique number
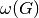 of a graph G is the number of
of a graph G is the number of - vertices in a maximum clique in G. The intersection number of
- G is the smallest number of cliques that together cover all edges of G.
- http (//en.wikipedia.org/wiki/Maximum_clique)
References
[1] Boppana, R., & Halldórsson, M. M. (1992). Approximating maximum independent sets by excluding subgraphs. BIT Numerical Mathematics, 32(2), 180–196. Springer. doi:10.1007/BF01994876