circulant_graph

circulant_graph(n, offsets, create_using=None)

Returns the circulant graph \(Ci_n(x_1, x_2, ..., x_m)\) with \(n\) nodes.

The circulant graph \(Ci_n(x_1, ..., x_m)\) consists of \(n\) nodes \(0, ..., n-1\) such that node \(i\) is connected to nodes \((i + x) \mod n\) and \((i - x) \mod n\) for all \(x\) in \(x_1, ..., x_m\). Thus \(Ci_n(1)\) is a cycle graph.

(Source code, png)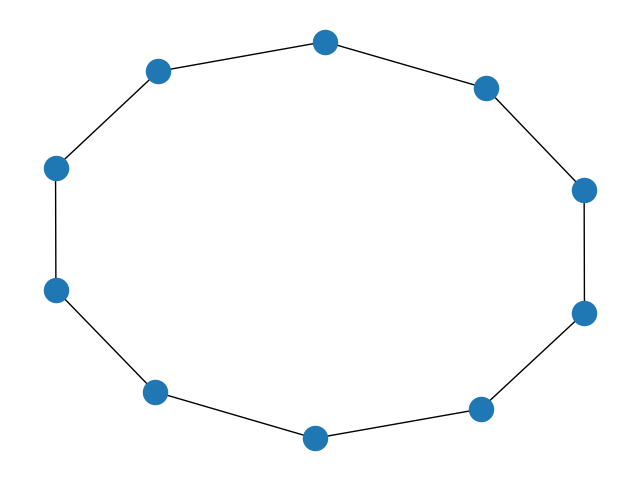

Parameters:

ninteger

The number of nodes in the graph.

offsetslist of integers

A list of node offsets, \(x_1\) up to \(x_m\), as described above.

create_usingNetworkX graph constructor, optional (default=nx.Graph)

Graph type to create. If graph instance, then cleared before populated.

Returns:

NetworkX Graph of type create_using

Examples

Many well-known graph families are subfamilies of the circulant graphs; for example, to create the cycle graph on n points, we connect every node to nodes on either side (with offset plus or minus one). For n = 10,

>>> G = nx.circulant_graph(10, [1])
>>> edges = [
...     (0, 9),
...     (0, 1),
...     (1, 2),
...     (2, 3),
...     (3, 4),
...     (4, 5),
...     (5, 6),
...     (6, 7),
...     (7, 8),
...     (8, 9),
... ]
>>> sorted(edges) == sorted(G.edges())
True

Similarly, we can create the complete graph on 5 points with the set of offsets [1, 2]:

>>> G = nx.circulant_graph(5, [1, 2])
>>> edges = [
...     (0, 1),
...     (0, 2),
...     (0, 3),
...     (0, 4),
...     (1, 2),
...     (1, 3),
...     (1, 4),
...     (2, 3),
...     (2, 4),
...     (3, 4),
... ]
>>> sorted(edges) == sorted(G.edges())
True