Note
Click here to download the full example code
Giant Component¶
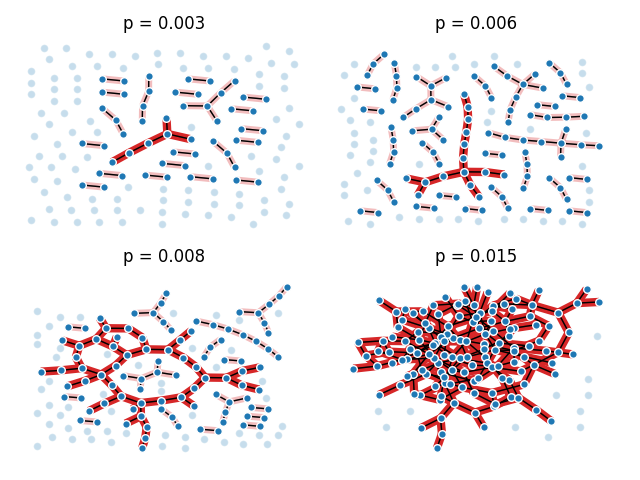
This example illustrates the sudden appearance of a giant connected component in a binomial random graph.
This example needs Graphviz and PyGraphviz.
import math
import matplotlib.pyplot as plt
import networkx as nx
n = 150 # 150 nodes
# p value at which giant component (of size log(n) nodes) is expected
p_giant = 1.0 / (n - 1)
# p value at which graph is expected to become completely connected
p_conn = math.log(n) / n
# the following range of p values should be close to the threshold
pvals = [0.003, 0.006, 0.008, 0.015]
fig, axes = plt.subplots(2, 2)
for p, ax, seed in zip(pvals, axes.ravel(), range(len(pvals))):
#### generate graph ####
G = nx.binomial_graph(n, p, seed=seed)
# identify connected/disconnected nodes
connected = [n for n, d in G.degree() if d > 0]
disconnected = list(set(G.nodes()) - set(connected))
# identify largest connected component
Gcc = sorted(nx.connected_components(G), key=len, reverse=True)
G0 = G.subgraph(Gcc[0])
#### draw graph ####
pos = nx.nx_agraph.graphviz_layout(G)
ax.set_title(f"p = {p:.3f}")
# draw largest connected component
options = {"ax": ax, "edge_color": "tab:red"}
nx.draw_networkx_edges(G0, pos, width=6.0, **options)
# draw other connected components
for Gi in Gcc[1:]:
if len(Gi) > 1:
nx.draw_networkx_edges(G.subgraph(Gi), pos, alpha=0.3, width=5.0, **options)
# draw connected/disconnected nodes
options = {"ax": ax, "node_size": 30, "edgecolors": "white"}
nx.draw(G, pos, nodelist=connected, **options)
nx.draw(G, pos, nodelist=disconnected, alpha=0.25, **options)
fig.tight_layout()
plt.show()
Total running time of the script: ( 0 minutes 0.777 seconds)