Warning
This documents an unmaintained version of NetworkX. Please upgrade to a maintained version and see the current NetworkX documentation.
navigable_small_world_graph¶
-
navigable_small_world_graph(n, p=1, q=1, r=2, dim=2, seed=None)[source]¶ Return a navigable small-world graph.
A navigable small-world graph is a directed grid with additional long-range connections that are chosen randomly.
[...] we begin with a set of nodes [...] that are identified with the set of lattice points in an
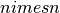 square,
square, 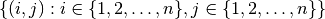 , and we define the lattice
distance between two nodes
, and we define the lattice
distance between two nodes 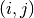 and
and 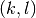 to be the number of
“lattice steps” separating them:
to be the number of
“lattice steps” separating them: 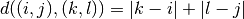 .
For a universal constant
.
For a universal constant 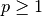 , the node
, the node 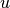 has a directed edge to
every other node within lattice distance
has a directed edge to
every other node within lattice distance 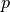 — these are its local
contacts. For universal constants
— these are its local
contacts. For universal constants 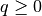 and
and 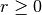 we also
construct directed edges from
we also
construct directed edges from 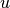 to
to 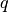 other nodes (the long-range
contacts) using independent random trials; the
other nodes (the long-range
contacts) using independent random trials; the 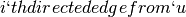 has endpoint
has endpoint  with probability proportional to
with probability proportional to ![[d(u,v)]^{-r}](../../_images/math/f9fffbbbe5557f330d1a70e32214a0525497341f.png) .
.—[1]
Parameters: - n (int) – The number of nodes.
- p (int) – The diameter of short range connections. Each node is joined with every other node within this lattice distance.
- q (int) – The number of long-range connections for each node.
- r (float) – Exponent for decaying probability of connections. The probability of
connecting to a node at lattice distance
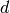 is
is 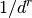 .
. - dim (int) – Dimension of grid
- seed (int, optional) – Seed for random number generator (default=None).
References
[1] J. Kleinberg. The small-world phenomenon: An algorithmic perspective. Proc. 32nd ACM Symposium on Theory of Computing, 2000.