projected_graph¶

projected_graph(B, nodes, multigraph=False)[source]¶

Returns the projection of B onto one of its node sets.

Returns the graph G that is the projection of the bipartite graph B onto the specified nodes. They retain their attributes and are connected in G if they have a common neighbor in B.

Parameters:	B (NetworkX graph) – The input graph should be bipartite. nodes (list or iterable) – Nodes to project onto (the “bottom” nodes). multigraph (bool (default=False)) – If True return a multigraph where the multiple edges represent multiple shared neighbors. They edge key in the multigraph is assigned to the label of the neighbor.
Returns:	Graph – A graph that is the projection onto the given nodes.
Return type:	NetworkX graph or multigraph

Examples

>>> from networkx.algorithms import bipartite
>>> B = nx.path_graph(4)
>>> G = bipartite.projected_graph(B, [1,3])
>>> print(G.nodes())
[1, 3]
>>> print(G.edges())
[(1, 3)]

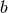If nodes $a$ , and $b$ are connected through both nodes 1 and 2 then building a multigraph results in two edges in the projection onto [ $a$ ,`b`]:

>>> B = nx.Graph()
>>> B.add_edges_from([('a', 1), ('b', 1), ('a', 2), ('b', 2)])
>>> G = bipartite.projected_graph(B, ['a', 'b'], multigraph=True)
>>> print([sorted((u,v)) for u,v in G.edges()])
[['a', 'b'], ['a', 'b']]

No attempt is made to verify that the input graph B is bipartite. Returns a simple graph that is the projection of the bipartite graph B onto the set of nodes given in list nodes. If multigraph=True then a multigraph is returned with an edge for every shared neighbor.

Directed graphs are allowed as input. The output will also then be a directed graph with edges if there is a directed path between the nodes.

The graph and node properties are (shallow) copied to the projected graph.