Warning
This documents an unmaintained version of NetworkX. Please upgrade to a maintained version and see the current NetworkX documentation.
collaboration_weighted_projected_graph¶
-
collaboration_weighted_projected_graph(B, nodes)[source]¶ Newman’s weighted projection of B onto one of its node sets.
The collaboration weighted projection is the projection of the bipartite network B onto the specified nodes with weights assigned using Newman’s collaboration model [1]:
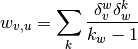
where
 and
and 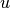 are nodes from the same bipartite node set,
and
are nodes from the same bipartite node set,
and 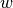 is a node of the opposite node set.
The value
is a node of the opposite node set.
The value 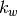 is the degree of node
is the degree of node 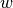 in the bipartite
network and
in the bipartite
network and 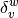 is 1 if node
is 1 if node  is
linked to node
is
linked to node 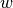 in the original bipartite graph or 0 otherwise.
in the original bipartite graph or 0 otherwise.The nodes retain their attributes and are connected in the resulting graph if have an edge to a common node in the original bipartite graph.
Parameters: - B (NetworkX graph) – The input graph should be bipartite.
- nodes (list or iterable) – Nodes to project onto (the “bottom” nodes).
Returns: Graph – A graph that is the projection onto the given nodes.
Return type: NetworkX graph
Examples
>>> from networkx.algorithms import bipartite >>> B = nx.path_graph(5) >>> B.add_edge(1,5) >>> G = bipartite.collaboration_weighted_projected_graph(B, [0, 2, 4, 5]) >>> print(G.nodes()) [0, 2, 4, 5] >>> for edge in G.edges(data=True): print(edge) ... (0, 2, {'weight': 0.5}) (0, 5, {'weight': 0.5}) (2, 4, {'weight': 1.0}) (2, 5, {'weight': 0.5})
No attempt is made to verify that the input graph B is bipartite. The graph and node properties are (shallow) copied to the projected graph.
See also
is_bipartite(),is_bipartite_node_set(),sets(),weighted_projected_graph(),overlap_weighted_projected_graph(),generic_weighted_projected_graph(),projected_graph()References
[1] Scientific collaboration networks: II. Shortest paths, weighted networks, and centrality, M. E. J. Newman, Phys. Rev. E 64, 016132 (2001).