Spectral Embedding

The spectral layout positions the nodes of the graph based on the eigenvectors of the graph Laplacian \(L = D - A\), where \(A\) is the adjacency matrix and \(D\) is the degree matrix of the graph. By default, the spectral layout will embed the graph in two dimensions (you can embed your graph in other dimensions using the dim argument to either draw_spectral() or spectral_layout()).

When the edges of the graph represent similarity between the incident nodes, the spectral embedding will place highly similar nodes closer to one another than nodes which are less similar.

This is particularly striking when you spectrally embed a grid graph. In the full grid graph, the nodes in the center of the graph are pulled apart more than nodes on the periphery. As you remove internal nodes, this effect increases.

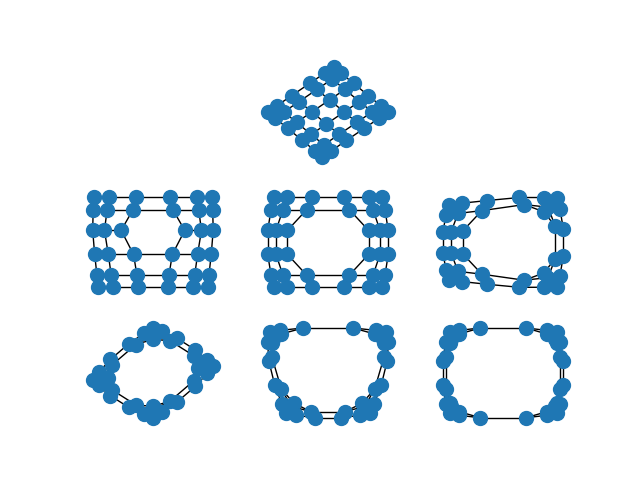
import matplotlib.pyplot as plt
import networkx as nx


options = {"node_color": "C0", "node_size": 100}

G = nx.grid_2d_graph(6, 6)
plt.subplot(332)
nx.draw_spectral(G, **options)

G.remove_edge((2, 2), (2, 3))
plt.subplot(334)
nx.draw_spectral(G, **options)

G.remove_edge((3, 2), (3, 3))
plt.subplot(335)
nx.draw_spectral(G, **options)

G.remove_edge((2, 2), (3, 2))
plt.subplot(336)
nx.draw_spectral(G, **options)

G.remove_edge((2, 3), (3, 3))
plt.subplot(337)
nx.draw_spectral(G, **options)

G.remove_edge((1, 2), (1, 3))
plt.subplot(338)
nx.draw_spectral(G, **options)

G.remove_edge((4, 2), (4, 3))
plt.subplot(339)
nx.draw_spectral(G, **options)

plt.show()