random_clustered_graph¶

random_clustered_graph(joint_degree_sequence, create_using=None, seed=None)[source]¶

Generate a random graph with the given joint independent edge degree and triangle degree sequence.

This uses a configuration model-like approach to generate a random graph (with parallel edges and self-loops) by randomly assigning edges to match the given joint degree sequence.

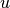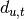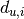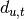The joint degree sequence is a list of pairs of integers of the form $[(d_{1,i}, d_{1,t}), \dotsc, (d_{n,i}, d_{n,t})]$ . According to this list, vertex $u$ is a member of $d_{u,t}$ triangles and has $d_{u, i}$ other edges. The number $d_{u,t}$ is the triangle degree of 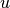$u$ and the number 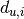$d_{u,i}$ is the independent edge degree.

Parameters:	joint_degree_sequence (list of integer pairs) – Each list entry corresponds to the independent edge degree and triangle degree of a node. create_using (graph, optional (default MultiGraph)) – Return graph of this type. The instance will be cleared. seed (hashable object, optional) – The seed for the random number generator.
Returns:	G – A graph with the specified degree sequence. Nodes are labeled starting at 0 with an index corresponding to the position in deg_sequence.
Return type:	MultiGraph
Raises:	`NetworkXError` – If the independent edge degree sequence sum is not even or the triangle degree sequence sum is not divisible by 3.

Notes

As described by Miller [1] (see also Newman [2] for an equivalent description).

A non-graphical degree sequence (not realizable by some simple graph) is allowed since this function returns graphs with self loops and parallel edges. An exception is raised if the independent degree sequence does not have an even sum or the triangle degree sequence sum is not divisible by 3.

This configuration model-like construction process can lead to duplicate edges and loops. You can remove the self-loops and parallel edges (see below) which will likely result in a graph that doesn’t have the exact degree sequence specified. This “finite-size effect” decreases as the size of the graph increases.

References

[1]	Joel C. Miller. “Percolation and epidemics in random clustered networks”. In: Physical review. E, Statistical, nonlinear, and soft matter physics 80 (2 Part 1 August 2009).

[2]	M. E. J. Newman. “Random Graphs with Clustering”. In: Physical Review Letters 103 (5 July 2009)

Examples

>>> deg = [(1, 0), (1, 0), (1, 0), (2, 0), (1, 0), (2, 1), (0, 1), (0, 1)]
>>> G = nx.random_clustered_graph(deg)

To remove parallel edges:

>>> G = nx.Graph(G)

To remove self loops:

>>> G.remove_edges_from(G.selfloop_edges())