clustering¶

clustering(G, nodes=None, weight=None)[source]¶

Compute the clustering coefficient for nodes.

For unweighted graphs, the clustering of a node 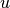$u$ is the fraction of possible triangles through that node that exist,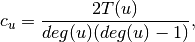

$c_u = \frac{2 T(u)}{deg(u)(deg(u)-1)},$

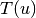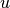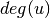where $T(u)$ is the number of triangles through node $u$ and $deg(u)$ is the degree of $u$ .

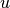For weighted graphs, the clustering is defined as the geometric average of the subgraph edge weights [1],

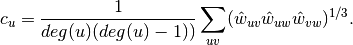
$c_u = \frac{1}{deg(u)(deg(u)-1))} \sum_{uv} (\hat{w}_{uv} \hat{w}_{uw} \hat{w}_{vw})^{1/3}.$

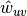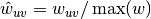The edge weights $\hat{w}_{uv}$ are normalized by the maximum weight in the network $\hat{w}_{uv} = w_{uv}/\max(w)$ .

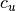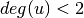The value of $c_u$ is assigned to 0 if $deg(u) < 2$ .

Parameters:	G (graph) – nodes (container of nodes, optional (default=all nodes in G)) – Compute clustering for nodes in this container. weight (string or None, optional (default=None)) – The edge attribute that holds the numerical value used as a weight. If None, then each edge has weight 1.
Returns:	out – Clustering coefficient at specified nodes
Return type:	float, or dictionary

Examples

>>> G=nx.complete_graph(5)
>>> print(nx.clustering(G,0))
1.0
>>> print(nx.clustering(G))
{0: 1.0, 1: 1.0, 2: 1.0, 3: 1.0, 4: 1.0}

Notes

Self loops are ignored.

References

[1]	Generalizations of the clustering coefficient to weighted complex networks by J. Saramäki, M. Kivelä, J.-P. Onnela, K. Kaski, and J. Kertész, Physical Review E, 75 027105 (2007). http://jponnela.com/web_documents/a9.pdf