Warning
This documents an unmaintained version of NetworkX. Please upgrade to a maintained version and see the current NetworkX documentation.
to_vertex_cover¶
-
to_vertex_cover(G, matching)[source]¶ Returns the minimum vertex cover corresponding to the given maximum matching of the bipartite graph
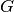 .
.Parameters: - G (NetworkX graph) – Undirected bipartite graph
- matching (dictionary) – A dictionary whose keys are vertices in
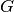 and whose values are the
distinct neighbors comprising the maximum matching for
and whose values are the
distinct neighbors comprising the maximum matching for 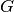 , as returned
by, for example,
, as returned
by, for example, maximum_matching(). The dictionary must represent the maximum matching.
Returns: vertex_cover –
The minimum vertex cover in
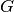 .
.Return type: Notes
This function is implemented using the procedure guaranteed by Konig’s theorem, which proves an equivalence between a maximum matching and a minimum vertex cover in bipartite graphs.
Since a minimum vertex cover is the complement of a maximum independent set for any graph, one can compute the maximum independent set of a bipartite graph this way:
>>> import networkx as nx >>> G = nx.complete_bipartite_graph(2, 3) >>> matching = nx.bipartite.maximum_matching(G) >>> vertex_cover = nx.bipartite.to_vertex_cover(G, matching) >>> independent_set = set(G) - vertex_cover >>> print(list(independent_set)) [2, 3, 4]