Directed Acyclic Graphs & Topological Sort#
In this tutorial, we will explore the algorithms related to a directed acyclic graph
(or a “DAG” as it is sometimes called) implemented in NetworkX under networkx/algorithms/dag.py.
First of all, we need to understand what a directed graph is.
Import packages#
import networkx as nx
import matplotlib.pyplot as plt
import inspect
%matplotlib inline
Example: Directed Graphs#
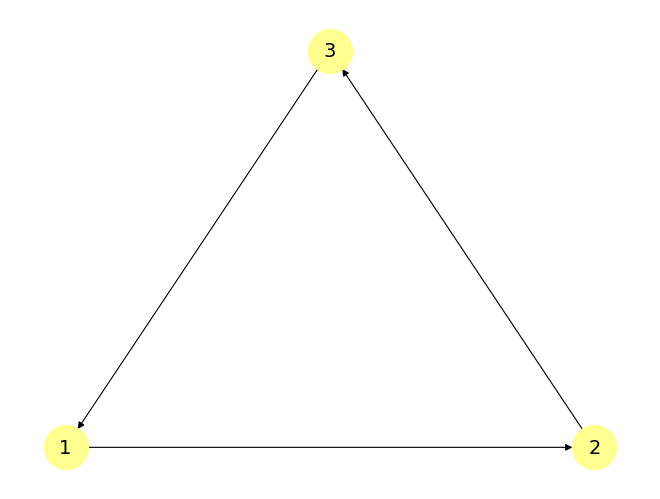
triangle_graph = nx.DiGraph([(1, 2), (2, 3), (3, 1)])
nx.draw_planar(
triangle_graph,
with_labels=True,
node_size=1000,
node_color="#ffff8f",
width=0.8,
font_size=14,
)
Definition#
In mathematics, and more specifically in graph theory, a directed graph (or DiGraph) is a graph that is made up of a set of vertices connected by directed edges often called arcs. Edges here have directionality, which stands in contrast to undirected graphs where, semantically, edges have no notion of a direction to them. Directed acyclic graphs take this idea further; by being acyclic, they have no cycles in them. You will see this idea in action in the examples below.
Directed Acyclic Graph#
Example#
clothing_graph = nx.read_graphml(f"data/clothing_graph.graphml")
plt.figure(figsize=(12, 12), dpi=150)
nx.draw_planar(
clothing_graph,
arrowsize=12,
with_labels=True,
node_size=8000,
node_color="#ffff8f",
linewidths=2.0,
width=1.5,
font_size=14,
)
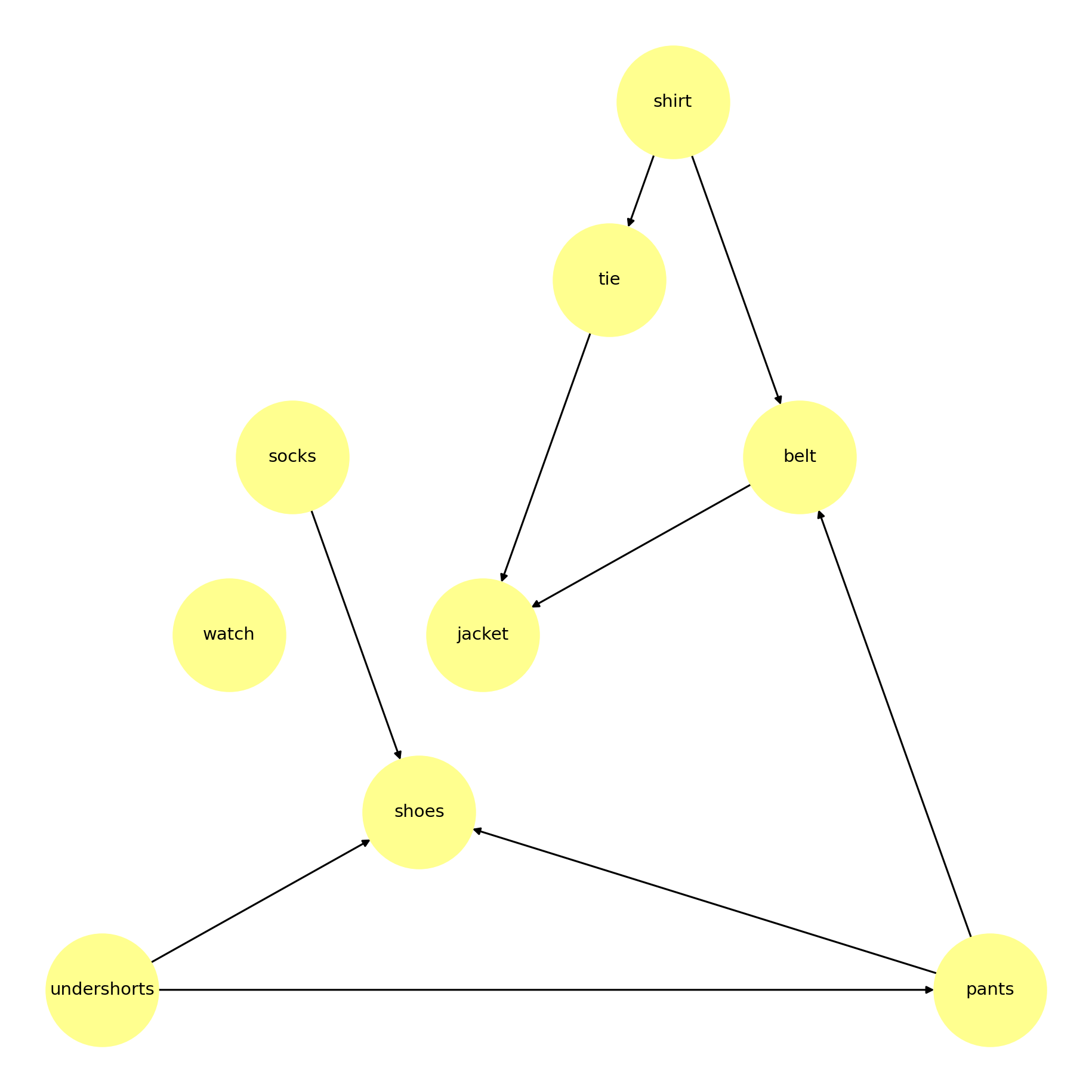
Here is a fun example of Professor Bumstead, who has a routine for getting dressed in the morning. By habit, the professor dons certain garments before others (e.g., socks before shoes). Other items may be put on in any order (e.g., socks and pants).
A directed edge \((u, v)\) in the example indicates that garment \(u\) must be donned before garment \(v\).
In this example, the clothing_graph is a DAG.
nx.is_directed_acyclic_graph(clothing_graph)
True
By contrast, the triangle_graph is not a DAG.
nx.is_directed_acyclic_graph(triangle_graph)
False
This is because the triangle_graph has a cycle:
nx.find_cycle(triangle_graph)
[(1, 2), (2, 3), (3, 1)]
Applications#
Directed acyclic graphs representations of partial orderings have many applications in scheduling of systems of tasks with ordering constraints. An important class of problems of this type concern collections of objects that need to be updated, for example, calculating the order of cells of a spreadsheet to update after one of the cells has been changed, or identifying which object files of software to update after its source code has been changed. In these contexts, we use a dependency graph, which is a graph that has a vertex for each object to be updated, and an edge connecting two objects whenever one of them needs to be updated earlier than the other. A cycle in this graph is called a circular dependency, and is generally not allowed, because there would be no way to consistently schedule the tasks involved in the cycle. Dependency graphs without circular dependencies form DAGs.
A directed acyclic graph may also be used to represent a network of processing elements. In this representation, data enters a processing element through its incoming edges and leaves the element through its outgoing edges. For instance, in electronic circuit design, static combinational logic blocks can be represented as an acyclic system of logic gates that computes a function of an input, where the input and output of the function are represented as individual bits.
Definition#
A directed acyclic graph (“DAG” or “dag”) is a directed graph with no directed cycles. That is, it consists of vertices and edges (also called arcs), with each edge directed from one vertex to another, such that following those directions will never form a closed loop.
A directed graph is a DAG if and only if it can be topologically ordered by arranging the vertices as a linear ordering that is consistent with all edge directions.
Topological sort#
Let’s now introduce what the topological sort is.
Example#
list(nx.topological_sort(clothing_graph))
['undershorts',
'shirt',
'socks',
'watch',
'pants',
'tie',
'belt',
'shoes',
'jacket']
Applications#
The canonical application of topological sorting is in scheduling a sequence of jobs or tasks based on their dependencies. The jobs are represented by vertices, and there is an edge from \(u\) to \(v\) if job \(u\) must be completed before job \(v\) can be started (for example, when washing clothes, the washing machine must finish before we put the clothes in the dryer). Then, a topological sort gives an order in which to perform the jobs.
A closely related application of topological sorting algorithms was first studied in the early 1960s in the context of the PERT technique [1] for scheduling in project management. In this application, the vertices of a graph represent the milestones of a project, and the edges represent tasks that must be performed between one milestone and another. Topological sorting forms the basis of linear-time algorithms for finding the critical path of the project, a sequence of milestones and tasks that controls the length of the overall project schedule.
In computer science, applications of this type arise in instruction scheduling, ordering of formula cell evaluation when recomputing formula values in spreadsheets, logic synthesis, determining the order of compilation tasks to perform in makefiles, data serialization, and resolving symbol dependencies in linkers. It is also used to decide in which order to load tables with foreign keys in databases.
Definition#
A topological sort of a directed acyclic graph \(G = (V, E)\) is a linear ordering of all its vertices such that if \(G\) contains an edge \((u, v)\), then \(u\) appears before \(v\) in the ordering.
It is worth noting that if the graph contains a cycle, then no linear ordering is possible.
It is useful to view a topological sort of a graph as an ordering of its vertices along a horizontal line so that all directed edges go from left to right.
Kahn’s algorithm#
NetworkX uses Kahn’s algorithm to perform topological sorting. We will introduce it briefly here.
First, find a list of “start nodes” which have no incoming edges and insert them into a set S; at least one such node must exist in a non-empty acyclic graph. Then:
L <- Empty list that will contain the sorted elements
S <- Set of all nodes with no incoming edge
while S is not empty do
remove a node N from S
add N to L
for each node M with an edge E from N to M do
remove edge E from the graph
if M has no other incoming edges then
insert M into S
if graph has edges then
return error # graph has at least one cycle
else
return L # a topologically sorted order
NetworkX implementation#
Finally, let’s take a look at how the topological sorting is implemented in NetworkX.
We can see that Kahn’s algorithm stratifies the graph such that each level contains all the nodes whose dependencies have been satisfied by the nodes in a previous level. In other words, Kahn’s algorithm does something like:
Take all the nodes in the DAG that don’t have any dependencies and put them in list.
“Remove” those nodes from the DAG.
Repeat the process, creating a new list at each step. Thus, topological sorting is reduced to correctly stratifying the graph in this way.
This procedure is implemented in the topological_generations() function, on which the topological_sort() function is based.
Let’s see how the topological_generations() function is implemented in NetworkX step by step.
Step 1. Initialize in-degrees.#
Since in Kahn’s algorithm we are only interested in the in-degrees of the vertices,
in order to preserve the structure of the graph as it is passed in,
instead of removing the edges, we will decrease the in-degree of the corresponding vertex.
Therefore, we will save these values in a separate dictionary indegree_map.
indegree_map = {v: d for v, d in G.in_degree() if d > 0}
Step 2. Initialize first level.#
At each step of Kahn’s algorithm, we seek out vertices with an in-degree of zero.
In preparation for the first loop iteration of the algorithm,
we can initialize a list called zero_indegree that houses these nodes:
zero_indegree = [v for v, d in G.in_degree() if d == 0]
Step 3. Move from one level to the next.#
Now, we will show how the algorithm moves from one level to the next.
Inside the loop, the first generation to be considered (this_generation)
is the collection of nodes that have zero in-degrees.
We process all the vertices of the current level in variable this_generation
and we store the next level in variable zero_indegree.
For each vertex inside this_generation,
we remove all of its outgoing edges.
Then, if the input degree of some vertex is zeroed as a result,
then we add it to the next level zero_indegree
and remove it from the indegree_map dictionary.
After we have processed all of the nodes inside this_generation, we can yield it.
while zero_indegree:
this_generation = zero_indegree
zero_indegree = []
for node in this_generation:
for child in G.neighbors(node):
indegree_map[child] -= 1
if indegree_map[child] == 0:
zero_indegree.append(child)
del indegree_map[child]
yield this_generation
Step 4. Check if there is a cycle in the graph.#
If, after completing the loop there are still vertices in the graph, then there is a cycle in it and the graph is not a DAG.
if indegree_map:
raise nx.NetworkXUnfeasible(
"Graph contains a cycle or graph changed during iteration"
)
Addendum: Topological sort works on multigraphs as well.#
This is possible to do by slightly modifying the algorithm above.
Firstly, check if
Gis a multigraphmultigraph = G.is_multigraph()
Then, replace
indegree_map[child] -= 1
with
indegree_map[child] -= len(G[node][child]) if multigraph else 1
Addendum: The graph may have changed during the iteration.#
Between passing different levels in a topological sort, the graph could change.
We need to check this while the while loop is running.
To do this, just replace
for node in this_generation: for child in G.neighbors(node): indegree_map[child] -= 1
with
for node in this_generation: if node not in G: raise RuntimeError("Graph changed during iteration") for child in G.neighbors(node): try: indegree_map[child] -= 1 except KeyError as e: raise RuntimeError("Graph changed during iteration") from e
Combine all steps.#
Combining all of the above gives the current implementation of the topological_generations() function in NetworkX.
print(inspect.getsource(nx.topological_generations))
@nx._dispatchable
def topological_generations(G):
"""Stratifies a DAG into generations.
A topological generation is node collection in which ancestors of a node in each
generation are guaranteed to be in a previous generation, and any descendants of
a node are guaranteed to be in a following generation. Nodes are guaranteed to
be in the earliest possible generation that they can belong to.
Parameters
----------
G : NetworkX digraph
A directed acyclic graph (DAG)
Yields
------
sets of nodes
Yields sets of nodes representing each generation.
Raises
------
NetworkXError
Generations are defined for directed graphs only. If the graph
`G` is undirected, a :exc:`NetworkXError` is raised.
NetworkXUnfeasible
If `G` is not a directed acyclic graph (DAG) no topological generations
exist and a :exc:`NetworkXUnfeasible` exception is raised. This can also
be raised if `G` is changed while the returned iterator is being processed
RuntimeError
If `G` is changed while the returned iterator is being processed.
Examples
--------
>>> DG = nx.DiGraph([(2, 1), (3, 1)])
>>> [sorted(generation) for generation in nx.topological_generations(DG)]
[[2, 3], [1]]
Notes
-----
The generation in which a node resides can also be determined by taking the
max-path-distance from the node to the farthest leaf node. That value can
be obtained with this function using `enumerate(topological_generations(G))`.
See also
--------
topological_sort
"""
if not G.is_directed():
raise nx.NetworkXError("Topological sort not defined on undirected graphs.")
multigraph = G.is_multigraph()
indegree_map = {v: d for v, d in G.in_degree() if d > 0}
zero_indegree = [v for v, d in G.in_degree() if d == 0]
while zero_indegree:
this_generation = zero_indegree
zero_indegree = []
for node in this_generation:
if node not in G:
raise RuntimeError("Graph changed during iteration")
for child in G.neighbors(node):
try:
indegree_map[child] -= len(G[node][child]) if multigraph else 1
except KeyError as err:
raise RuntimeError("Graph changed during iteration") from err
if indegree_map[child] == 0:
zero_indegree.append(child)
del indegree_map[child]
yield this_generation
if indegree_map:
raise nx.NetworkXUnfeasible(
"Graph contains a cycle or graph changed during iteration"
)
Let’s finally see what the result will be on the clothing_graph.
list(nx.topological_generations(clothing_graph))
[['undershorts', 'shirt', 'socks', 'watch'],
['pants', 'tie'],
['belt', 'shoes'],
['jacket']]
