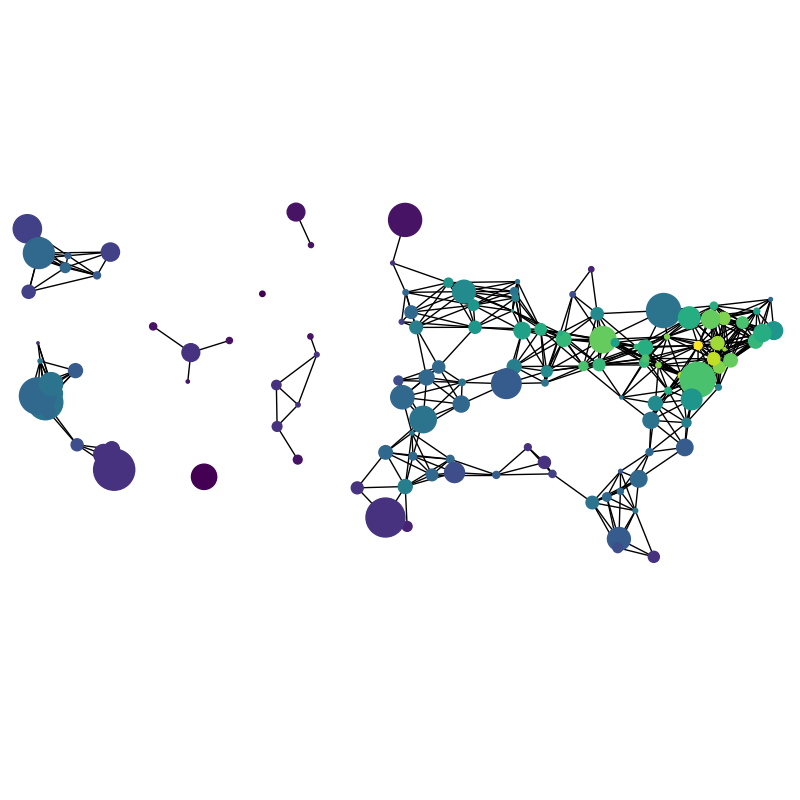
Knuth Miles

miles_graph() returns an undirected graph over the 128 US cities from. The cities each have location and population data. The edges are labeled with the distance between the two cities.

This example is described in Section 1.1 of

Donald E. Knuth, “The Stanford GraphBase: A Platform for Combinatorial Computing”, ACM Press, New York, 1993. http://www-cs-faculty.stanford.edu/~knuth/sgb.html

The data file can be found at:

• https://github.com/networkx/networkx/blob/master/examples/drawing/knuth_miles.txt.gz

Out:

Loaded miles_dat.txt containing 128 cities.
digraph has 128 nodes with 8128 edges

import gzip
import re

import matplotlib.pyplot as plt
import networkx as nx


def miles_graph():
    """ Return the cites example graph in miles_dat.txt
        from the Stanford GraphBase.
    """
    # open file miles_dat.txt.gz (or miles_dat.txt)

    fh = gzip.open("knuth_miles.txt.gz", "r")

    G = nx.Graph()
    G.position = {}
    G.population = {}

    cities = []
    for line in fh.readlines():
        line = line.decode()
        if line.startswith("*"):  # skip comments
            continue

        numfind = re.compile(r"^\d+")

        if numfind.match(line):  # this line is distances
            dist = line.split()
            for d in dist:
                G.add_edge(city, cities[i], weight=int(d))
                i = i + 1
        else:  # this line is a city, position, population
            i = 1
            (city, coordpop) = line.split("[")
            cities.insert(0, city)
            (coord, pop) = coordpop.split("]")
            (y, x) = coord.split(",")

            G.add_node(city)
            # assign position - flip x axis for matplotlib, shift origin
            G.position[city] = (-int(x) + 7500, int(y) - 3000)
            G.population[city] = float(pop) / 1000.0
    return G


G = miles_graph()

print("Loaded miles_dat.txt containing 128 cities.")
print(f"digraph has {nx.number_of_nodes(G)} nodes with {nx.number_of_edges(G)} edges")

# make new graph of cites, edge if less then 300 miles between them
H = nx.Graph()
for v in G:
    H.add_node(v)
for (u, v, d) in G.edges(data=True):
    if d["weight"] < 300:
        H.add_edge(u, v)

# draw with matplotlib/pylab
plt.figure(figsize=(8, 8))
# with nodes colored by degree sized by population
node_color = [float(H.degree(v)) for v in H]
nx.draw(
    H,
    G.position,
    node_size=[G.population[v] for v in H],
    node_color=node_color,
    with_labels=False,
)

# scale the axes equally
plt.xlim(-5000, 500)
plt.ylim(-2000, 3500)

plt.show()