Atlas

Atlas of all graphs of 6 nodes or less.

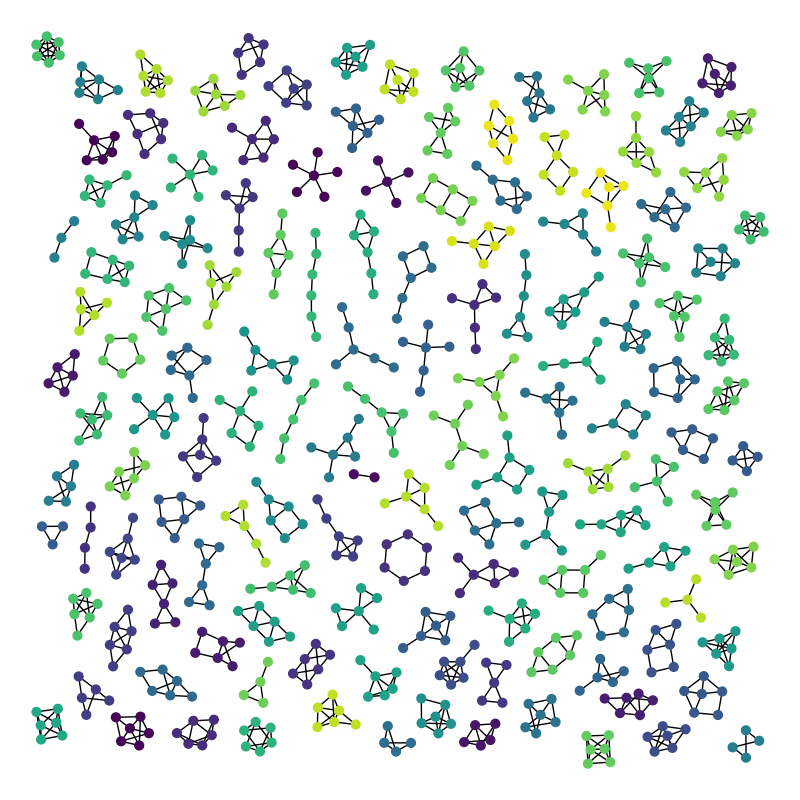
Out:

graph has 779 nodes with 1073 edges
137 connected components

import random

# This example needs Graphviz and either PyGraphviz or pydot.
# from networkx.drawing.nx_pydot import graphviz_layout
from networkx.drawing.nx_agraph import graphviz_layout

import matplotlib.pyplot as plt

import networkx as nx
from networkx.algorithms.isomorphism.isomorph import (
    graph_could_be_isomorphic as isomorphic,
)
from networkx.generators.atlas import graph_atlas_g


def atlas6():
    """ Return the atlas of all connected graphs of 6 nodes or less.
        Attempt to check for isomorphisms and remove.
    """

    Atlas = graph_atlas_g()[0:208]  # 208
    # remove isolated nodes, only connected graphs are left
    U = nx.Graph()  # graph for union of all graphs in atlas
    for G in Atlas:
        zerodegree = [n for n in G if G.degree(n) == 0]
        for n in zerodegree:
            G.remove_node(n)
        U = nx.disjoint_union(U, G)

    # iterator of graphs of all connected components
    C = (U.subgraph(c) for c in nx.connected_components(U))

    UU = nx.Graph()
    # do quick isomorphic-like check, not a true isomorphism checker
    nlist = []  # list of nonisomorphic graphs
    for G in C:
        # check against all nonisomorphic graphs so far
        if not iso(G, nlist):
            nlist.append(G)
            UU = nx.disjoint_union(UU, G)  # union the nonisomorphic graphs
    return UU


def iso(G1, glist):
    """Quick and dirty nonisomorphism checker used to check isomorphisms."""
    for G2 in glist:
        if isomorphic(G1, G2):
            return True
    return False


G = atlas6()

print(f"graph has {nx.number_of_nodes(G)} nodes with {nx.number_of_edges(G)} edges")
print(nx.number_connected_components(G), "connected components")

plt.figure(1, figsize=(8, 8))
# layout graphs with positions using graphviz neato
pos = graphviz_layout(G, prog="neato")
# color nodes the same in each connected subgraph
C = (G.subgraph(c) for c in nx.connected_components(G))
for g in C:
    c = [random.random()] * nx.number_of_nodes(g)  # random color...
    nx.draw(g, pos, node_size=40, node_color=c, vmin=0.0, vmax=1.0, with_labels=False)
plt.show()