normalized_laplacian_matrix¶
- normalized_laplacian_matrix(G, nodelist=None, weight='weight')[source]¶
Return the normalized Laplacian matrix of G.
The normalized graph Laplacian is the matrix
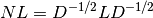
where
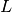 is the graph Laplacian and
is the graph Laplacian and 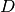 is the diagonal matrix of
node degrees.
is the diagonal matrix of
node degrees.Parameters : G : graph
A NetworkX graph
nodelist : list, optional
The rows and columns are ordered according to the nodes in nodelist. If nodelist is None, then the ordering is produced by G.nodes().
weight : string or None, optional (default=’weight’)
The edge data key used to compute each value in the matrix. If None, then each edge has weight 1.
Returns : L : NumPy matrix
The normalized Laplacian matrix of G.
See also
Notes
For MultiGraph/MultiDiGraph, the edges weights are summed. See to_numpy_matrix for other options.
If the Graph contains selfloops, D is defined as diag(sum(A,1)), where A is the adjencency matrix [R295].
References
[R294] Fan Chung-Graham, Spectral Graph Theory, CBMS Regional Conference Series in Mathematics, Number 92, 1997. [R295] (1, 2) Steve Butler, Interlacing For Weighted Graphs Using The Normalized Laplacian, Electronic Journal of Linear Algebra, Volume 16, pp. 90-98, March 2007.