directed_laplacian_matrix¶
- directed_laplacian_matrix(G, nodelist=None, weight='weight', walk_type=None, alpha=0.95)[source]¶
Return the directed Laplacian matrix of G.
The graph directed Laplacian is the matrix
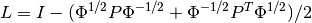
where
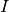 is the identity matrix,
is the identity matrix, 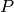 is the transition matrix of the
graph, and
is the transition matrix of the
graph, and 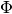 a matrix with the Perron vector of
a matrix with the Perron vector of 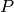 in the diagonal and
zeros elsewhere.
in the diagonal and
zeros elsewhere.Depending on the value of walk_type,
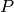 can be the transition matrix
induced by a random walk, a lazy random walk, or a random walk with
teleportation (PageRank).
can be the transition matrix
induced by a random walk, a lazy random walk, or a random walk with
teleportation (PageRank).Parameters : G : DiGraph
A NetworkX graph
nodelist : list, optional
The rows and columns are ordered according to the nodes in nodelist. If nodelist is None, then the ordering is produced by G.nodes().
weight : string or None, optional (default=’weight’)
The edge data key used to compute each value in the matrix. If None, then each edge has weight 1.
walk_type : string or None, optional (default=None)
If None,
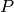 is selected depending on the properties of the
graph. Otherwise is one of ‘random’, ‘lazy’, or ‘pagerank’
is selected depending on the properties of the
graph. Otherwise is one of ‘random’, ‘lazy’, or ‘pagerank’alpha : real
(1 - alpha) is the teleportation probability used with pagerank
Returns : L : NumPy array
Normalized Laplacian of G.
Raises : NetworkXError :
If NumPy cannot be imported
NetworkXNotImplemnted :
If G is not a DiGraph
See also
Notes
Only implemented for DiGraphs
References
[R293] Fan Chung (2005). Laplacians and the Cheeger inequality for directed graphs. Annals of Combinatorics, 9(1), 2005