node_connectivity

node_connectivity(G, s=None, t=None)

Returns node connectivity for a graph or digraph G.

Node connectivity is equal to the minimum number of nodes that must be removed to disconnect G or render it trivial. If source and target nodes are provided, this function returns the local node connectivity: the minimum number of nodes that must be removed to break all paths from source to target in G.

This is a flow based implementation. The algorithm is based in solving a number of max-flow problems (ie local st-node connectivity, see local_node_connectivity) to determine the capacity of the minimum cut on an auxiliary directed network that corresponds to the minimum node cut of G. It handles both directed and undirected graphs.

Parameters :

G : NetworkX graph

Undirected graph

s : node

Source node. Optional (default=None)

t : node

Target node. Optional (default=None)

Returns :

K : integer

Node connectivity of G, or local node connectivity if source and target were provided

See also

local_node_connectivity, all_pairs_node_connectivity_matrix, local_edge_connectivity, edge_connectivity, max_flow, ford_fulkerson

Notes

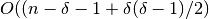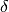This is a flow based implementation of node connectivity. The algorithm works by solving max-flow problems on an auxiliary digraph. Where is the minimum degree of G. For details about the auxiliary digraph and the computation of local node connectivity see local_node_connectivity.

This implementation is based on algorithm 11 in [R202]. We use the Ford and Fulkerson algorithm to compute max flow (see ford_fulkerson).

References

[R202]

(1, 2) Abdol-Hossein Esfahanian. Connectivity Algorithms. http://www.cse.msu.edu/~cse835/Papers/Graph_connectivity_revised.pdf

Examples

>>> # Platonic icosahedral graph is 5-node-connected 
>>> G = nx.icosahedral_graph()
>>> nx.node_connectivity(G)
5
>>> nx.node_connectivity(G, 3, 7)
5