local_node_connectivity

local_node_connectivity(G, s, t, aux_digraph=None, mapping=None)

Computes local node connectivity for nodes s and t.

Local node connectivity for two non adjacent nodes s and t is the minimum number of nodes that must be removed (along with their incident edges) to disconnect them.

This is a flow based implementation of node connectivity. We compute the maximum flow on an auxiliary digraph build from the original input graph (see below for details). This is equal to the local node connectivity because the value of a maximum s-t-flow is equal to the capacity of a minimum s-t-cut (Ford and Fulkerson theorem) [R201] .

Parameters :

G : NetworkX graph

Undirected graph

s : node

Source node

t : node

Target node

aux_digraph : NetworkX DiGraph (default=None)

Auxiliary digraph to compute flow based node connectivity. If None the auxiliary digraph is build.

mapping : dict (default=None)

Dictionary with a mapping of node names in G and in the auxiliary digraph.

Returns :

K : integer

local node connectivity for nodes s and t

See also

node_connectivity, all_pairs_node_connectivity_matrix, local_edge_connectivity, edge_connectivity, max_flow, ford_fulkerson

Notes

This is a flow based implementation of node connectivity. We compute the maximum flow using the Ford and Fulkerson algorithm on an auxiliary digraph build from the original input graph:

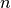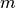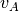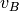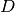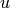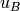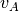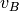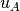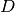For an undirected graph G having nodes and edges we derive a directed graph D with 2n nodes and 2m+n arcs by replacing each original node with two nodes , linked by an (internal) arc in . Then for each edge (, ) in G we add two arcs (, ) and (, ) in . Finally we set the attribute capacity = 1 for each arc in 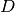[R201] .

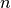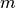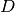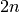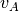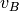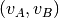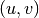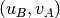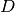For a directed graph G having nodes and arcs we derive a directed graph with nodes and arcs by replacing each original node with two nodes , linked by an (internal) arc in D. Then for each arc in G we add one arc in . Finally we set the attribute capacity = 1 for each arc in .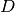

This is equal to the local node connectivity because the value of a maximum s-t-flow is equal to the capacity of a minimum s-t-cut (Ford and Fulkerson theorem).

References

[R201]

(1, 2, 3) Kammer, Frank and Hanjo Taubig. Graph Connectivity. in Brandes and Erlebach, ‘Network Analysis: Methodological Foundations’, Lecture Notes in Computer Science, Volume 3418, Springer-Verlag, 2005. http://www.informatik.uni-augsburg.de/thi/personen/kammer/Graph_Connectivity.pdf

Examples

>>> # Platonic icosahedral graph has node connectivity 5 
>>> # for each non adjacent node pair
>>> G = nx.icosahedral_graph()
>>> nx.local_node_connectivity(G,0,6)
5