rich_club_coefficient

rich_club_coefficient(G, normalized=True, Q=100)

Return the rich-club coefficient of the graph G.

The rich-club coefficient is the ratio, for every degree k, of the number of actual to the number of potential edges for nodes with degree greater than k:

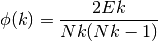
where Nk is the number of nodes with degree larger than k, and Ek be the number of edges among those nodes.

Parameters :

G : NetworkX graph

normalized : bool (optional)

Normalize using randomized network (see [R199])

Q : float (optional, default=100)

If normalized=True build a random network by performing Q*M double-edge swaps, where M is the number of edges in G, to use as a null-model for normalization.

Returns :

rc : dictionary

A dictionary, keyed by degree, with rich club coefficient values.

Notes

The rich club definition and algorithm are found in [R199]. This algorithm ignores any edge weights and is not defined for directed graphs or graphs with parallel edges or self loops.

Estimates for appropriate values of Q are found in [R200].

References

[R199]

(1, 2, 3) Julian J. McAuley, Luciano da Fontoura Costa, and Tibério S. Caetano, “The rich-club phenomenon across complex network hierarchies”, Applied Physics Letters Vol 91 Issue 8, August 2007. http://arxiv.org/abs/physics/0701290

[R200]

(1, 2) R. Milo, N. Kashtan, S. Itzkovitz, M. E. J. Newman, U. Alon, “Uniform generation of random graphs with arbitrary degree sequences”, 2006. http://arxiv.org/abs/cond-mat/0312028

Examples

>>> G = nx.Graph([(0,1),(0,2),(1,2),(1,3),(1,4),(4,5)])
>>> rc = nx.rich_club_coefficient(G,normalized=False)
>>> rc[0] 
0.4