biconnected_components

biconnected_components(G)

Return a generator of sets of nodes, one set for each biconnected component of the graph

Biconnected components are maximal subgraphs such that the removal of a node (and all edges incident on that node) will not disconnect the subgraph. Note that nodes may be part of more than one biconnected component. Those nodes are articulation points, or cut vertices. The removal of articulation points will increase the number of connected components of the graph.

Notice that by convention a dyad is considered a biconnected component.

Parameters :

G : NetworkX Graph

An undirected graph.

Returns :

nodes : generator

Generator of sets of nodes, one set for each biconnected component.

Raises :

NetworkXError : :

If the input graph is not undirected.

See also

is_biconnected, articulation_points, biconnected_component_edges, biconnected_component_subgraphs

Notes

The algorithm to find articulation points and biconnected components is implemented using a non-recursive depth-first-search (DFS) that keeps track of the highest level that back edges reach in the DFS tree. A node 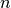is an articulation point if, and only if, there exists a subtree rooted at 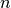such that there is no back edge from any successor of 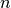that links to a predecessor of 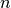in the DFS tree. By keeping track of all the edges traversed by the DFS we can obtain the biconnected components because all edges of a bicomponent will be traversed consecutively between articulation points.

References

[R164]

Hopcroft, J.; Tarjan, R. (1973). “Efficient algorithms for graph manipulation”. Communications of the ACM 16: 372–378. doi:10.1145/362248.362272

Examples

>>> G = nx.barbell_graph(4,2)
>>> print(nx.is_biconnected(G))
False
>>> components = nx.biconnected_components(G)
>>> G.add_edge(2,8)
>>> print(nx.is_biconnected(G))
True
>>> components = nx.biconnected_components(G)