clustering¶

clustering(G, nodes=None, mode='dot')[source]¶

Compute a bipartite clustering coefficient for nodes.

The bipartie clustering coefficient is a measure of local density of connections defined as [R122]

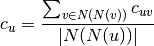
$c_u = \frac{\sum_{v \in N(N(v))} c_{uv} }{|N(N(u))|}$

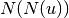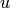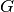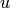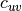where $N(N(u))$ are the second order neighbors of $u$ in $G$ excluding $u$ , and $c_{uv}$ is the pairwise clustering coefficient between nodes 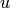$u$ and $v$ .

The mode selects the function for 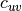$c_{uv}$ ‘dot’: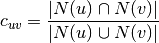

$c_{uv}=\frac{|N(u)\cap N(v)|}{|N(u) \cup N(v)|}$

‘min’:

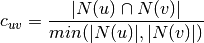
$c_{uv}=\frac{|N(u)\cap N(v)|}{min(|N(u)|,|N(v)|)}$

‘max’:

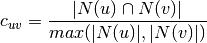
$c_{uv}=\frac{|N(u)\cap N(v)|}{max(|N(u)|,|N(v)|)}$

Parameters :

G : graph

A bipartite graph

nodes : list or iterable (optional)

Compute bipartite clustering for these nodes. The default is all nodes in G.

mode : string

The pariwise bipartite clustering method to be used in the computation. It must be “dot”, “max”, or “min”.

Returns :

clustering : dictionary

A dictionary keyed by node with the clustering coefficient value.

See also

average_clustering

References

[R122]

(1, 2) Latapy, Matthieu, Clémence Magnien, and Nathalie Del Vecchio (2008). Basic notions for the analysis of large two-mode networks. Social Networks 30(1), 31–48.

Examples

>>> from networkx.algorithms import bipartite
>>> G=nx.path_graph(4) # path is bipartite
>>> c=bipartite.clustering(G) 
>>> c[0]
0.5
>>> c=bipartite.clustering(G,mode='min') 
>>> c[0]
1.0

Previous topic

Next topic

clustering¶

Navigation

Previous topic

Next topic

Quick search

clustering¶

Navigation