degree_centrality

degree_centrality(G, nodes)

Compute the degree centrality for nodes in a bipartite network.

The degree centrality for a node is the fraction of nodes connected to it.

Parameters :

G : graph

A bipartite network

nodes : list or container

Container with all nodes in one bipartite node set.

Returns :

centrality : dictionary

Dictionary keyed by node with bipartite degree centrality as the value.

See also

betweenness_centrality, closeness_centrality, sets, is_bipartite

Notes

The nodes input parameter must conatin all nodes in one bipartite node set, but the dictionary returned contains all nodes from both bipartite node sets.

For unipartite networks, the degree centrality values are normalized by dividing by the maximum possible degree (which is 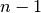where 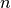is the number of nodes in G).

In the bipartite case, the maximum possible degree of a node in a bipartite node set is the number of nodes in the opposite node set [R120]. The degree centrality for a node in the bipartite sets 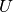with 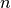nodes and 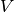with 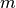nodes is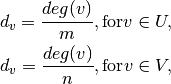

where 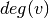is the degree of node .

References

[R120]

(1, 2) Borgatti, S.P. and Halgin, D. In press. “Analyzing Affiliation Networks”. In Carrington, P. and Scott, J. (eds) The Sage Handbook of Social Network Analysis. Sage Publications. http://www.steveborgatti.com/papers/bhaffiliations.pdf