Approximation¶
Clique¶
Cliques.
| max_clique(graph) | Find the Maximum Clique |
| clique_removal(graph) | Repeatedly remove cliques from the graph. |
Dominating Set¶
A dominating set for a graph G = (V, E) is a subset D of V such that every vertex not in D is joined to at least one member of D by some edge. The domination number gamma(G) is the number of vertices in a smallest dominating set for G. Given a graph G = (V, E) find a minimum weight dominating set V’.
http://en.wikipedia.org/wiki/Dominating_set
This is reducible to the minimum set dom_set problem.
| min_weighted_dominating_set(graph[, weight]) | Return minimum weight dominating set. |
| min_edge_dominating_set(graph) | Return minimum weight dominating edge set. |
Independent Set¶
Independent Set
Independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I. The size of an independent set is the number of vertices it contains.
A maximum independent set is a largest independent set for a given graph G and its size is denoted α(G). The problem of finding such a set is called the maximum independent set problem and is an NP-hard optimization problem. As such, it is unlikely that there exists an efficient algorithm for finding a maximum independent set of a graph.
http://en.wikipedia.org/wiki/Independent_set_(graph_theory)
Independent set algorithm is based on the following paper:
 apx of maximum clique/independent set.
apx of maximum clique/independent set.
Boppana, R., & Halldórsson, M. M. (1992). Approximating maximum independent sets by excluding subgraphs. BIT Numerical Mathematics, 32(2), 180–196. Springer. doi:10.1007/BF01994876
| maximum_independent_set(graph) | Return an approximate maximum independent set. |
Matching¶
Given a graph G = (V,E), a matching M in G is a set of pairwise non-adjacent edges; that is, no two edges share a common vertex.
http://en.wikipedia.org/wiki/Matching_(graph_theory)
| min_maximal_matching(graph) | Returns a set of edges such that no two edges share a common endpoint and every edge not in the set shares some common endpoint in the set. |
Vertex Cover¶
Given an undirected graph 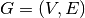 and a function w assigning nonnegative
weights to its vertices, find a minimum weight subset of V such that each edge
in E is incident to at least one vertex in the subset.
and a function w assigning nonnegative
weights to its vertices, find a minimum weight subset of V such that each edge
in E is incident to at least one vertex in the subset.
http://en.wikipedia.org/wiki/Vertex_cover
| min_weighted_vertex_cover(graph[, weight]) | 2-OPT Local Ratio for Minimum Weighted Vertex Cover |
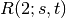 for graph.
for graph.