random_geometric_graph

random_geometric_graph(n, radius, dim=2, pos=None)

Return the random geometric graph in the unit cube.

The random geometric graph model places n nodes uniformly at random in the unit cube Two nodes 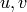are connected with an edge if 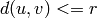where 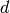is the Euclidean distance and is a radius threshold.

Parameters :

n : int

Number of nodes

radius: float :

Distance threshold value

dim : int, optional

Dimension of graph

pos : dict, optional

A dictionary keyed by node with node positions as values.

Returns :

Graph :

Notes

This uses an 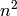algorithm to build the graph. A faster algorithm is possible using k-d trees.

The pos keyword can be used to specify node positions so you can create an arbitrary distribution and domain for positions. If you need a distance function other than Euclidean you’ll have to hack the algorithm.

E.g to use a 2d Gaussian distribution of node positions with mean (0,0) and std. dev. 2

>>> import random
>>> n=20
>>> p=dict((i,(random.gauss(0,2),random.gauss(0,2))) for i in range(n))
>>> G = nx.random_geometric_graph(n,0.2,pos=p)

References

[R202]

Penrose, Mathew, Random Geometric Graphs, Oxford Studies in Probability, 5, 2003.

Examples

>>> G = nx.random_geometric_graph(20,0.1)