Giant Component¶

#!/usr/bin/env python
"""
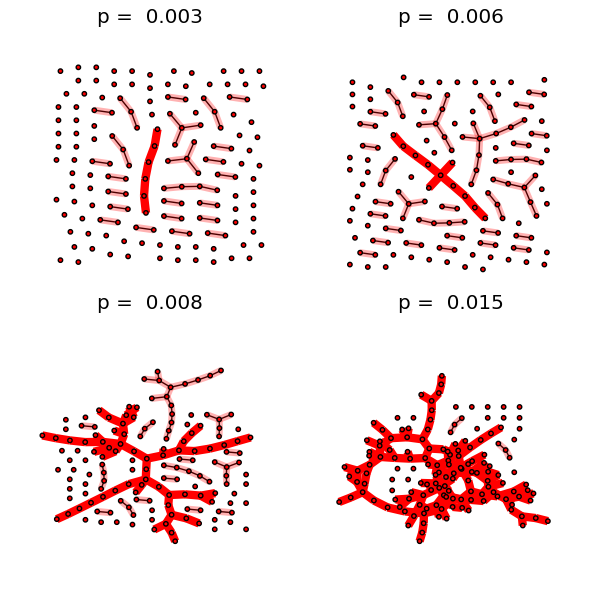
This example illustrates the sudden appearance of a
giant connected component in a binomial random graph.

Requires pygraphviz and matplotlib to draw.

"""
#    Copyright (C) 2006-2008
#    Aric Hagberg <hagberg@lanl.gov>
#    Dan Schult <dschult@colgate.edu>
#    Pieter Swart <swart@lanl.gov>
#    All rights reserved.
#    BSD license.

try:
    import matplotlib.pyplot as plt
except:
    raise

import networkx as nx
import math

try:
    from networkx import graphviz_layout
    layout=nx.graphviz_layout
except ImportError:
    print "PyGraphviz not found; drawing with spring layout; will be slow."
    layout=nx.spring_layout


n=150  # 150 nodes
# p value at which giant component (of size log(n) nodes) is expected
p_giant=1.0/(n-1)
# p value at which graph is expected to become completely connected
p_conn=math.log(n)/float(n)

# the following range of p values should be close to the threshold
pvals=[0.003, 0.006, 0.008, 0.015]

region=220 # for pylab 2x2 subplot layout
plt.subplots_adjust(left=0,right=1,bottom=0,top=0.95,wspace=0.01,hspace=0.01)
for p in pvals:
    G=nx.binomial_graph(n,p)
    pos=layout(G)
    region+=1
    plt.subplot(region)
    plt.title("p = %6.3f"%(p))
    nx.draw(G,pos,
            with_labels=False,
            node_size=10
            )
    # identify largest connected component
    Gcc=sorted(nx.connected_component_subgraphs(G), key = len, reverse=True)
    G0=Gcc[0]
    nx.draw_networkx_edges(G0,pos,
                           with_labels=False,
                           edge_color='r',
                           width=6.0
                        )
    # show other connected components
    for Gi in Gcc[1:]:
       if len(Gi)>1:
          nx.draw_networkx_edges(Gi,pos,
                                 with_labels=False,
                                 edge_color='r',
                                 alpha=0.3,
                                 width=5.0
                                 )
plt.savefig("giant_component.png")
plt.show() # display