clustering

clustering(G, nodes=None, weight=None)

Compute the clustering coefficient for nodes.

For unweighted graphs, the clustering of a node 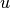is the fraction of possible triangles through that node that exist,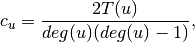

where 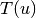is the number of triangles through node 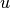and 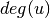is the degree of .

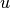For weighted graphs, the clustering is defined as the geometric average of the subgraph edge weights [R185],

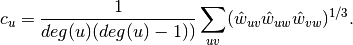
The edge weights 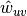are normalized by the maximum weight in the network .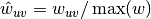

The value of 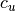is assigned to 0 if .

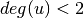Parameters :

G : graph

nodes : container of nodes, optional (default=all nodes in G)

Compute clustering for nodes in this container.

weight : string or None, optional (default=None)

The edge attribute that holds the numerical value used as a weight. If None, then each edge has weight 1.

Returns :

out : float, or dictionary

Clustering coefficient at specified nodes

Notes

Self loops are ignored.

References

[R185]

(1, 2) Generalizations of the clustering coefficient to weighted complex networks by J. Saramäki, M. Kivelä, J.-P. Onnela, K. Kaski, and J. Kertész, Physical Review E, 75 027105 (2007). http://jponnela.com/web_documents/a9.pdf

Examples

>>> G=nx.complete_graph(5)
>>> print(nx.clustering(G,0))
1.0
>>> print(nx.clustering(G))
{0: 1.0, 1: 1.0, 2: 1.0, 3: 1.0, 4: 1.0}