betweenness_centrality¶
- betweenness_centrality(G, k=None, normalized=True, weight=None, endpoints=False, seed=None)¶
Compute the shortest-path betweenness centrality for nodes.
Betweenness centrality of a node
 is the sum of the
fraction of all-pairs shortest paths that pass through
is the sum of the
fraction of all-pairs shortest paths that pass through  :
: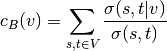
where
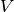 is the set of nodes,
is the set of nodes, 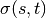 is the number of
shortest
is the number of
shortest 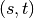 -paths, and
-paths, and 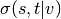 is the number of those
paths passing through some node
is the number of those
paths passing through some node  other than
other than 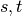 .
If
.
If 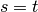 ,
, 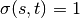 , and if
, and if 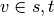 ,
,
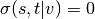 [R155].
[R155].Parameters : G : graph
A NetworkX graph
k : int, optional (default=None)
If k is not None use k node samples to estimate betweenness. The value of k <= n where n is the number of nodes in the graph. Higher values give better approximation.
normalized : bool, optional
If True the betweenness values are normalized by
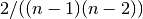 for graphs, and
for graphs, and 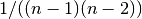 for directed graphs where
for directed graphs where 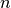 is the number of nodes in G.
is the number of nodes in G.weight : None or string, optional
If None, all edge weights are considered equal. Otherwise holds the name of the edge attribute used as weight.
endpoints : bool, optional
If True include the endpoints in the shortest path counts.
Returns : nodes : dictionary
Dictionary of nodes with betweenness centrality as the value.
See also
Notes
The algorithm is from Ulrik Brandes [R154]. See [R155] for details on algorithms for variations and related metrics.
For approximate betweenness calculations set k=#samples to use k nodes (“pivots”) to estimate the betweenness values. For an estimate of the number of pivots needed see [R156].
For weighted graphs the edge weights must be greater than zero. Zero edge weights can produce an infinite number of equal length paths between pairs of nodes.
References
[R154] (1, 2) A Faster Algorithm for Betweenness Centrality. Ulrik Brandes, Journal of Mathematical Sociology 25(2):163-177, 2001. http://www.inf.uni-konstanz.de/algo/publications/b-fabc-01.pdf [R155] (1, 2, 3) Ulrik Brandes: On Variants of Shortest-Path Betweenness Centrality and their Generic Computation. Social Networks 30(2):136-145, 2008. http://www.inf.uni-konstanz.de/algo/publications/b-vspbc-08.pdf [R156] (1, 2) Ulrik Brandes and Christian Pich: Centrality Estimation in Large Networks. International Journal of Bifurcation and Chaos 17(7):2303-2318, 2007. http://www.inf.uni-konstanz.de/algo/publications/bp-celn-06.pdf