average_neighbor_degree¶
- average_neighbor_degree(G, source='out', target='out', nodes=None, weight=None)¶
Returns the average degree of the neighborhood of each node.
The average degree of a node
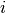 is
is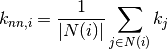
where
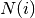 are the neighbors of node
are the neighbors of node 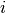 and
and 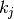 is
the degree of node
is
the degree of node 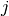 which belongs to
which belongs to 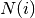 . For weighted
graphs, an analogous measure can be defined [R133],
. For weighted
graphs, an analogous measure can be defined [R133],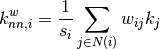
where
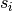 is the weighted degree of node
is the weighted degree of node 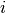 ,
, 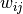 is the weight of the edge that links
is the weight of the edge that links 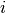 and
and 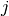 and
and
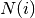 are the neighbors of node
are the neighbors of node 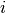 .
.Parameters : G : NetworkX graph
source : string (“in”|”out”)
Directed graphs only. Use “in”- or “out”-degree for source node.
target : string (“in”|”out”)
Directed graphs only. Use “in”- or “out”-degree for target node.
nodes : list or iterable, optional
Compute neighbor degree for specified nodes. The default is all nodes in the graph.
weight : string or None, optional (default=None)
The edge attribute that holds the numerical value used as a weight. If None, then each edge has weight 1.
Returns : d: dict :
A dictionary keyed by node with average neighbors degree value.
See also
Notes
For directed graphs you can also specify in-degree or out-degree by passing keyword arguments.
References
[R133] (1, 2) A. Barrat, M. Barthélemy, R. Pastor-Satorras, and A. Vespignani, “The architecture of complex weighted networks”. PNAS 101 (11): 3747–3752 (2004). Examples
>>> G=nx.path_graph(4) >>> G.edge[0][1]['weight'] = 5 >>> G.edge[2][3]['weight'] = 3
>>> nx.average_neighbor_degree(G) {0: 2.0, 1: 1.5, 2: 1.5, 3: 2.0} >>> nx.average_neighbor_degree(G, weight='weight') {0: 2.0, 1: 1.1666666666666667, 2: 1.25, 3: 2.0}
>>> G=nx.DiGraph() >>> G.add_path([0,1,2,3]) >>> nx.average_neighbor_degree(G, source='in', target='in') {0: 1.0, 1: 1.0, 2: 1.0, 3: 0.0}
>>> nx.average_neighbor_degree(G, source='out', target='out') {0: 1.0, 1: 1.0, 2: 0.0, 3: 0.0}