flow_hierarchy

flow_hierarchy(G, weight=None)

Returns the flow hierarchy of a directed network.

Flow hierarchy is defined as the fraction of edges not participating in cycles in a directed graph [R228].

Parameters :

G : DiGraph or MultiDiGraph

A directed graph

weight : key,optional (default=None)

Attribute to use for node weights. If None the weight defaults to 1.

Returns :

h : float

Flow heirarchy value

Notes

The algorithm described in [R228] computes the flow hierarchy through exponentiation of the adjacency matrix. This function implements an alternative approach that finds strongly connected components. An edge is in a cycle if and only if it is in a strongly connected component, which can be found in 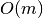time using Tarjan’s algorithm.

References

[R228]

(1, 2, 3) Luo, J.; Magee, C.L. (2011), Detecting evolving patterns of self-organizing networks by flow hierarchy measurement, Complexity, Volume 16 Issue 6 53-61. DOI: 10.1002/cplx.20368 http://web.mit.edu/~cmagee/www/documents/28-DetectingEvolvingPatterns_FlowHierarchy.pdf