ford_fulkerson_flow_and_auxiliary

ford_fulkerson_flow_and_auxiliary(G, s, t, capacity='capacity')

Find a maximum single-commodity flow using the Ford-Fulkerson algorithm.

This function returns both the value of the maximum flow and the auxiliary network resulting after finding the maximum flow, which is also named residual network in the literature. The auxiliary network has edges with capacity equal to the capacity of the edge in the original network minus the flow that went throught that edge. Notice that it can happen that a flow from v to u is allowed in the auxiliary network, though disallowed in the original network. A dictionary with infinite capacity edges can be found as an attribute of the auxiliary network.

Parameters :

G : NetworkX graph

Edges of the graph are expected to have an attribute called ‘capacity’. If this attribute is not present, the edge is considered to have infinite capacity.

s : node

Source node for the flow.

t : node

Sink node for the flow.

capacity: string :

Edges of the graph G are expected to have an attribute capacity that indicates how much flow the edge can support. If this attribute is not present, the edge is considered to have infinite capacity. Default value: ‘capacity’.

Returns :

flow_value : integer, float

Value of the maximum flow, i.e., net outflow from the source.

auxiliary : DiGraph

Residual/auxiliary network after finding the maximum flow. A dictionary with infinite capacity edges can be found as an attribute of this network: auxiliary.graph[‘inf_capacity_flows’]

Raises :

NetworkXError :

The algorithm does not support MultiGraph and MultiDiGraph. If the input graph is an instance of one of these two classes, a NetworkXError is raised.

NetworkXUnbounded :

If the graph has a path of infinite capacity, the value of a feasible flow on the graph is unbounded above and the function raises a NetworkXUnbounded.

Notes

This algorithm uses Edmonds-Karp-Dinitz path selection rule which guarantees a running time of for 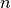nodes and 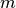edges.

Examples

>>> import networkx as nx
>>> G = nx.DiGraph()
>>> G.add_edge('x','a', capacity=3.0)
>>> G.add_edge('x','b', capacity=1.0)
>>> G.add_edge('a','c', capacity=3.0)
>>> G.add_edge('b','c', capacity=5.0)
>>> G.add_edge('b','d', capacity=4.0)
>>> G.add_edge('d','e', capacity=2.0)
>>> G.add_edge('c','y', capacity=2.0)
>>> G.add_edge('e','y', capacity=3.0)
>>> flow, auxiliary = nx.ford_fulkerson_flow_and_auxiliary(G, 'x', 'y')
>>> flow
3.0
>>> # A dictionary with infinite capacity flows can be found as an
>>> # attribute of the auxiliary network
>>> inf_capacity_flows = auxiliary.graph['inf_capacity_flows']