katz_centrality_numpy

katz_centrality_numpy(G, alpha=0.1, beta=1.0, normalized=True)

Compute the Katz centrality for the graph G.

Katz centrality is related to eigenvalue centrality and PageRank. The Katz centrality for node 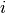is

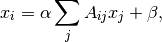
where 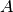is the adjacency matrix of the graph G with eigenvalues .

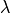The parameter 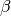controls the initial centrality and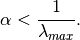

Katz centrality computes the relative influence of a node within a network by measuring the number of the immediate neighbors (first degree nodes) and also all other nodes in the network that connect to the node under consideration through these immediate neighbors.

Extra weight can be provided to immediate neighbors through the parameter 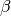. Connections made with distant neighbors are, however, penalized by an attenuation factor 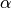which should be strictly less than the inverse largest eigenvalue of the adjacency matrix in order for the Katz centrality to be computed correctly. More information is provided in [R176] .

Parameters :

G : graph

A NetworkX graph

alpha : float

Attenuation factor

beta : scalar or dictionary, optional (default=1.0)

Weight attributed to the immediate neighborhood. If not a scalar the dictionary must have an value for every node.

normalized : bool

If True normalize the resulting values.

Returns :

nodes : dictionary

Dictionary of nodes with Katz centrality as the value.

See also

katz_centrality, eigenvector_centrality_numpy, eigenvector_centrality, pagerank, hits

Notes

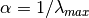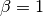This algorithm uses a direct linear solver to solve the above equation. The constant alpha should be strictly less than the inverse of largest eigenvalue of the adjacency matrix for there to be a solution. When and Katz centrality is the same as eigenvector centrality.

References

[R176]

(1, 2) M. Newman, Networks: An Introduction. Oxford University Press, USA, 2010, p. 720.

Examples

>>> import math
>>> G = nx.path_graph(4)
>>> phi = (1+math.sqrt(5))/2.0 # largest eigenvalue of adj matrix
>>> centrality = nx.katz_centrality_numpy(G,1/phi)
>>> for n,c in sorted(centrality.items()):
...    print("%d %0.2f"%(n,c))
0 0.37
1 0.60
2 0.60
3 0.37