biadjacency_matrix¶
- biadjacency_matrix(G, row_order, column_order=None, weight='weight', dtype=None)[source]¶
Return the biadjacency matrix of the bipartite graph G.
Let
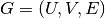 be a bipartite graph with node sets
be a bipartite graph with node sets
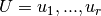 and
and 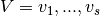 . The biadjacency
matrix [1] is the
. The biadjacency
matrix [1] is the  x
x  matrix
matrix 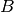 in which
in which 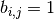 if, and only if,
if, and only if, 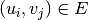 . If the parameter
. If the parameter 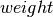 is
not
is
not 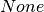 and matches the name of an edge attribute, its value is
used instead of 1.
and matches the name of an edge attribute, its value is
used instead of 1.Parameters : G : graph
A NetworkX graph
row_order : list of nodes
The rows of the matrix are ordered according to the list of nodes.
column_order : list, optional
The columns of the matrix are ordered according to the list of nodes. If column_order is None, then the ordering of columns is arbitrary.
weight : string or None, optional (default=’weight’)
The edge data key used to provide each value in the matrix. If None, then each edge has weight 1.
dtype : NumPy data type, optional
A valid single NumPy data type used to initialize the array. This must be a simple type such as int or numpy.float64 and not a compound data type (see to_numpy_recarray) If None, then the NumPy default is used.
Returns : B : numpy matrix
Biadjacency matrix representation of the bipartite graph G.
See also
to_numpy_matrix, adjacency_matrix
Notes
No attempt is made to check that the input graph is bipartite.
For directed bipartite graphs only successors are considered as neighbors. To obtain an adjacency matrix with ones (or weight values) for both predecessors and successors you have to generate two biadjacency matrices where the rows of one of them are the columns of the other, and then add one to the transpose of the other.
References
[1] http://en.wikipedia.org/wiki/Adjacency_matrix#Adjacency_matrix_of_a_bipartite_graph