clustering

clustering(G, nodes=None, weight=None)

Compute the clustering coefficient for nodes.

For unweighted graphs the clustering of each node 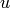is the fraction of possible triangles that exist, For each node find the fraction of possible triangles that exist,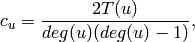

where 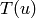is the number of triangles through node 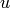and 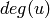is the degree of .

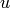For weighted graphs the clustering is defined as the geometric average of the subgraph edge weights [R143],

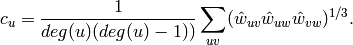
The edge weights 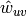are normalized by the maximum weight in the network .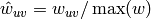

The value of 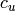is assigned to 0 if .

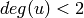Parameters :

G : graph

nodes : container of nodes, optional (default=all nodes in G)

Compute clustering for nodes in this container.

weight : string or None, optional (default=None)

The edge attribute that holds the numerical value used as a weight. If None, then each edge has weight 1.

Returns :

out : float, or dictionary

Clustering coefficient at specified nodes

Notes

Self loops are ignored.

References

[R143]

(1, 2) Generalizations of the clustering coefficient to weighted complex networks by J. Saramäki, M. Kivelä, J.-P. Onnela, K. Kaski, and J. Kertész, Physical Review E, 75 027105 (2007). http://jponnela.com/web_documents/a9.pdf

Examples

>>> G=nx.complete_graph(5)
>>> print(nx.clustering(G,0))
1.0
>>> print(nx.clustering(G))
{0: 1.0, 1: 1.0, 2: 1.0, 3: 1.0, 4: 1.0}