overlap_weighted_projected_graph

overlap_weighted_projected_graph(B, nodes, jaccard=True)

Return the overlap weighted projection of B onto the nodes of one bipartite node set.

The overlap weighted projection is the projection of the bipartite network B onto the specified nodes with weights representing the Jaccard index between the neighborhoods of the two nodes in the original bipartite network [R109]:

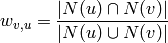
or if the parameter ‘jaccard’ is False, the fraction of common neighbors by minimum of both nodes degree in the original bipartite graph [R109]:

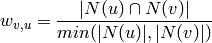
The nodes retain their names and are connected in the resulting graph if have an edge to a common node in the original bipartite graph.

Parameters :

B : NetworkX graph

The input graph should be bipartite.

nodes : list or iterable

Nodes to project onto (the “bottom” nodes).

jaccard: Bool (default=True) :

Returns :

Graph : NetworkX graph

A graph that is the projection onto the given nodes.

See also

is_bipartite, is_bipartite_node_set, sets, weighted_projected_graph, collaboration_weighted_projected_graph, generic_weighted_projected_graph, projected_graph

Notes

No attempt is made to verify that the input graph B is bipartite. The graph and node properties are (shallow) copied to the projected graph.

References

[R109]

(1, 2, 3) Borgatti, S.P. and Halgin, D. In press. Analyzing Affiliation Networks. In Carrington, P. and Scott, J. (eds) The Sage Handbook of Social Network Analysis. Sage Publications.

Examples

>>> from networkx.algorithms import bipartite
>>> B = nx.path_graph(5)
>>> G = bipartite.overlap_weighted_projected_graph(B, [0, 2, 4])
>>> print(G.nodes())
[0, 2, 4]
>>> print(G.edges(data=True))
[(0, 2, {'weight': 0.5}), (2, 4, {'weight': 0.5})]
>>> G = bipartite.overlap_weighted_projected_graph(B, [0, 2, 4], jaccard=False)
>>> print(G.edges(data=True))
[(0, 2, {'weight': 1.0}), (2, 4, {'weight': 1.0})]