networkx.generators.degree_seq.li_smax_graph

networkx.generators.degree_seq.li_smax_graph(degree_seq, create_using=None)

Generates a graph based with a given degree sequence and maximizing the s-metric. Experimental implementation.

Maximum s-metrix means that high degree nodes are connected to high degree nodes.

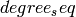• : degree sequence, a list of integers with each entry

  corresponding to the degree of a node. A non-graphical degree sequence raises an Exception.

Reference:

@unpublished{li-2005,
 author = {Lun Li and David Alderson and Reiko Tanaka
          and John C. Doyle and Walter Willinger},
 title = {Towards a Theory of Scale-Free Graphs:
         Definition, Properties, and  Implications (Extended Version)},
 url = {http://arxiv.org/abs/cond-mat/0501169},
 year = {2005}
}

The algorithm:

STEP 0 - Initialization
A = {0}
B = {1, 2, 3, ..., n}
O = {(i; j), ..., (k, l),...} where i < j, i <= k < l and 
        d_i * d_j >= d_k *d_l 
wA = d_1
dB = sum(degrees)

STEP 1 - Link selection
(a) If |O| = 0 TERMINATE. Return graph A.
(b) Select element(s) (i, j) in O having the largest d_i * d_j , if for 
        any i or j either w_i = 0 or w_j = 0 delete (i, j) from O
(c) If there are no elements selected go to (a).
(d) Select the link (i, j) having the largest value w_i (where for each 
        (i, j) w_i is the smaller of w_i and w_j ), and proceed to STEP 2.

STEP 2 - Link addition
Type 1: i in A and j in B. 
        Add j to the graph A and remove it from the set B add a link 
        (i, j) to the graph A. Update variables:
        wA = wA + d_j -2 and dB = dB - d_j
        Decrement w_i and w_j with one. Delete (i, j) from O
Type 2: i and j in A.
    Check Tree Condition: If dB = 2 * |B| - wA. 
        Delete (i, j) from O, continue to STEP 3
    Check Disconnected Cluster Condition: If wA = 2. 
        Delete (i, j) from O, continue to STEP 3
    Add the link (i, j) to the graph A 
    Decrement w_i and w_j with one, and wA = wA -2
STEP 3
    Go to STEP 1

The article states that the algorithm will result in a maximal s-metric. This implementation can not guarantee such maximality. I may have misunderstood the algorithm, but I can not see how it can be anything but a heuristic. Please contact me at sundsdal@gmail.com if you can provide python code that can guarantee maximality. Several optimizations are included in this code and it may be hard to read. Commented code to come.

A POSSIBLE ALTERNATIVE:

For an ‘unconstrained’ graph, that is one they describe as having the sum of the degree sequence be even(ie all undirected graphs) they present a simpler algorithm. It is as follows

“For each vertex i: if di is even then attach di/2 self-loops; if di is odd, then attach (di-1)/2 self-loops, leaving one available “stub”. Second for all remaining vertices with “stubs” connect them in pairs according to decreasing values of di.”[1]

Since this only works for undirected graphs anyway, perhaps this is the better method? Note this also returns a graph with a larger s_metric than the other method, and it seems to have the same degree sequence, though I haven’t tested it extensively.