networkx.algorithms.neighbor_degree.average_neighbor_degree

networkx.algorithms.neighbor_degree.average_neighbor_degree(G, nodes=None, weighted=False)

Returns the average degree of the neighborhood of each node.

The average degree of a node 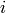is

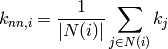
where 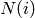are the neighbors of node 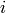and 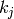is the degree of node 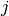which belongs to 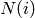. For weighted graphs, an analogous measure can be defined [R142],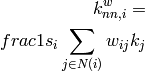

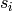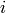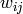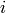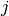where is the weighted degree of node , is the weight of the edge that links and and 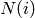are the neighbors of node .

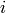Parameters :

G : NetworkX graph

nodes: list or iterable (optional) :

Compute neighbor connectivity for these nodes. The default is all nodes.

weighted: bool (default=False) :

Compute weighted average nearest neighbors degree.

Returns :

d: dict :

A dictionary keyed by node with average neighbors degree value.

See also

average_neighbor_out_degree, average_neighbor_in_degree, average_degree_connectivity

Notes

For directed graphs you can also specify in-degree or out-degree by calling the relevant functions.

References

[R142]

(1, 2) A. Barrat, M. Barthélemy, R. Pastor-Satorras, and A. Vespignani, “The architecture of complex weighted networks”. PNAS 101 (11): 3747–3752 (2004).

Examples

>>> G=nx.path_graph(4)
>>> G.edge[0][1]['weight'] = 5
>>> G.edge[2][3]['weight'] = 3
>>> nx.average_neighbor_degree(G)
{0: 2.0, 1: 1.5, 2: 1.5, 3: 2.0}
>>> nx.average_neighbor_degree(G, weighted=True)
{0: 2.0, 1: 1.1666666666666667, 2: 1.25, 3: 2.0}

>>> G=nx.DiGraph()
>>> G.add_path([0,1,2,3])
>>> nx.average_neighbor_in_degree(G)
{0: 1.0, 1: 1.0, 2: 1.0, 3: 0.0}
>>> nx.average_neighbor_out_degree(G)
{0: 1.0, 1: 1.0, 2: 0.0, 3: 0.0}