networkx.algorithms.centrality.edge_betweenness_centrality¶

networkx.algorithms.centrality.edge_betweenness_centrality(G, normalized=True, weighted_edges=False)¶

Compute betweenness centrality for edges.

Betweenness centrality of an edge $e$ is the sum of the fraction of all-pairs shortest paths that pass through $e$ :

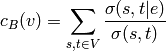
$c_B(v) =\sum_{s,t \in V} \frac{\sigma(s, t|e)}{\sigma(s, t)}$

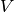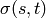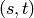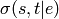where $V$ is the set of nodes, $\sigma(s, t)$ is the number of shortest $(s, t)$ -paths, and $\sigma(s, t|e)$ is the number of those paths passing through edge $e$ [R59]..

Parameters :

G : graph

A NetworkX graph

normalized : bool, optional

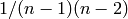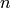If True the betweenness values are normalized by $1/(n-1)(n-2)$ where $n$ is the number of nodes in G.

weighted_edges : bool, optional

Consider the edge weights in determining the shortest paths. The edge weights must be greater than zero. If False, all edge weights are considered equal.

Returns :

edges : dictionary

Dictionary of edges with betweenness centrality as the value.

Previous topic

Next topic

networkx.algorithms.centrality.edge_betweenness_centrality¶

Navigation

Previous topic

Next topic

Quick search

networkx.algorithms.centrality.edge_betweenness_centrality¶

Navigation